2015-05-18
1731
Обобщенный метод наименьших квадратов (ОМНК) применяется в том случае, если нарушены предпосылки 2 и 3 классической линейной модели регрессии, т. е. случайные возмущения не имеют постоянной дисперсии или коррелированы между собой. В этом случае имеет место обобщенная линейная модель множественной регрессии.
Обобщенная регрессионная модель имеет следующую спецификацию:
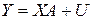. (3.3.1)
Здесь переменные и параметры определены так же, как в п. 2.1.
Относительно случайных возмущений регрессии принимаются следующие предпосылки:
;
,
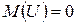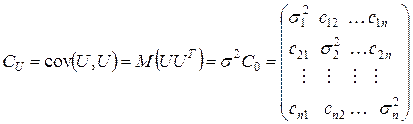где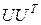 
– векторное произведение векторов; T – знак транспонирования матрицы, 
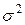– неизвестная положительная константа; 
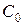– некоторая симметричная положительно определенная (корреляционная) матрица, которая полагается известной.
Таким образом, обобщенная модель отличается от классической только видом ковариационной матрицы возмущений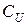 
. В классической модели предполагается, что матрица 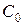равна единичной матрице. В обобщенной модели допускается, что ковариации остатков могут быть произвольными, т. е. 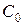может содержать произвольные значения.
Если применить к системе уравнений наблюдений (3.3.1) обычный МНК, то полученная МНК-оценка вектора коэффициентов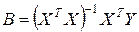 
и в условиях обобщенной модели остается состоятельной и несмещенной. Однако данные оценки будут неэффективными. Для преодоления этих последствий используется обобщенный МНК, применение которого основано на следующей теореме.
Теорема Айткена. В классе линейных несмещенных оценок вектора параметров обобщенной регрессионной модели оценка
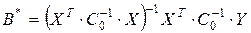(3.3.2)
является эффективной, т. е. имеет наименьшую ковариационную матрицу.
Ковариационная матрица МНК-оценок параметров регрессии (которая используется для определения дисперсий и стандартных ошибок оценок параметров) рассчитывается по формуле
.
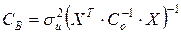Для применения ОМНК необходимо знать ковариационную матрицу случайных возмущений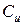 
, которая, как правило, неизвестна. Поэтому для практической реализации метода необходимо ввести дополнительные условия на структуру матрицы 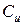, оценить каким-либо образом матрицу, а затем использовать эту оценку в формуле (3.3.2) вместо 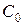. Данный подход составляет суть доступного обобщенного метода наименьших квадратов.
Линейная модель с гетероскедастичным возмущением является частным случаем ОЛММР. В этом случае на структуру матрицы 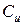наиболее часто накладывается следующее условие: среднее квадратическое отклонение возмущения пропорционально одной из факторных переменных 
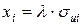. В этом случае ковариационная матрица имеет вид
.
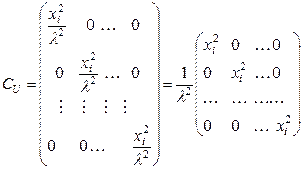При наличии автокорреляции возмущений при сохранении свойства гомоскедастичности делают предположение о том, что случайные составляющие связаны автокорреляционной зависимостью 1-го порядка: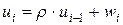 
, где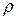 
– некоторая постоянная, 
; 
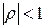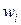– случайные величины, удовлетворяющие требованиям, предъявляемым к возмущениям классической модели. Ковариационная матрица в этом случае имеет вид
.
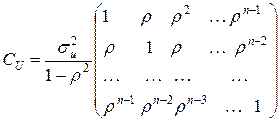1. Каковы условия применения обобщенного метода наименьших квадратов?
2. Сформулируйте теорему Айткена.
