Тест Голдфельда-Квандта

При проведении проверки по этому критерию предполагается, что стандартное отклонение 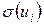возмущения пропорционально значению независимой переменной 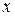. Предполагается также, что случайный член распределен нормально.

Все 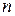наблюдений в выборке упорядочиваются по возрастанию переменной 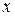. Затем оцениваются “частные” регрессии для первых 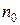и для последних 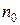наблюдений. Средние 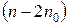наблюдений отбрасываются.

Нулевая гипотеза о равенстве дисперсий двух наборов по 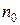наблюдений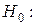 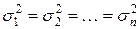(гипотеза об отсутствии гетероскедастичности) проверяется с помощью критерия Фишера-Снедекора.

Составляется статистика .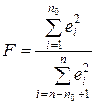

Если верна гипотеза 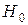об отсутствии гетероскедастичности, то F имеет распределение Фишера с двумя параметрами 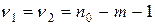, где m – число объясняющих переменных. По таблице F -распределения для уровня значимости 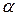определяется .

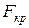Если 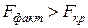, то нулевая гипотеза отвергается и делается вывод о гетероскедастичности случайного возмущения.

Пример 3.1.2

Проверить наличие гетероскедастичности данных из примера 3.1.1 при помощи теста Голдфельда-Квандта.

Решение. Поскольку число наблюдений в выборке n = 16, число наблюдений в “частных” регрессиях примем равным 7. Остатки двух частных регрессий вычислим с помощью функции ЛИНЕЙН Excel. Оценки регрессии по первым 7 и по последним 7 наблюдениям приведены ниже.

Таблица 3.1.3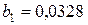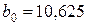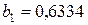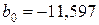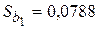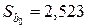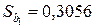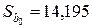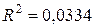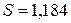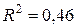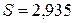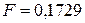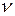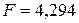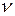




	=5		=5

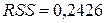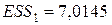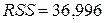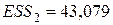Подставив суммы квадратов остатков первой и последней “частных” регрессий, равные 7,01 и 43,08 соответственно, в тестовую статистику, получим

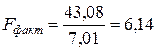По таблице F -распределения с двумя параметрами 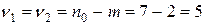для уровня значимости 0,05 критическое значение равно 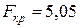. Таким образом, нулевая гипотеза об отсутствии гетероскедастичности отвергается.