2015-05-18
850
Наблюдаемая случайная переменная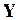 
, которую называют регрессандом, может быть представлена линейной функцией от 
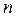наблюдаемых переменных 
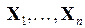, называемых регрессорами, и от скрытых (латентных) случайных переменных 
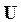, называемых случайными возмущениями
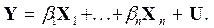
Функция называется регрессионной[1]. Имеющийся ряд наблюдений по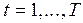 
позволяет для каждого наблюдения получить соотношение
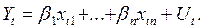(I. 1)
Вероятностный характер возмущений делает регрессионную функцию стохастической.
Ряды данных (наблюдений) длиной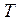 
для регрессанда и каждого из регрессоров необходимы для того, чтобы оценить параметры модели статистически. Количество рядов равно 
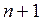в каждом 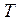точек наблюдения[2]:
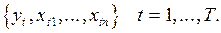
Длина временных рядов 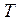образует так называемый опорный базовый период оценки.
Таким образом, для каждого из наблюдений имеем следующие соотношения:
.
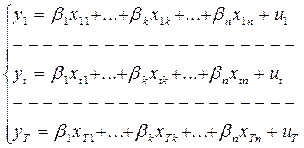Обозначая 
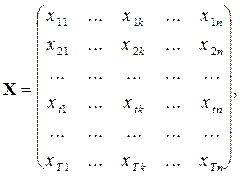
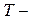мерный 
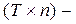мерная матрица
вектор
,
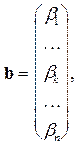
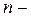мерный 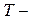мерный
вектор вектор
выше приведенное соотношение можно переписать в векторной форме: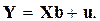 
Матрицу вида 
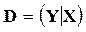будем называть матрицей данных.
При формировании матрицы данных, значения измеряемых величин “шкалируются” относительно фиксированных значений одного из регрессоров (например, первого).
Выражение вида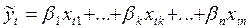 
называют систематической частью регрессанда.
