Для аддитивной модели фактическое значение A = трендовое значение T + сезонная вариация S + ошибка Е.
Пример 5. В таблице указан объем продаж (тыс. руб.) за последние 11 кварталов. Дадим на основании этих данных прогноз объема продаж на следующие два квартала.
| Квартал | |||||||||||
| Объем продаж |
На первом шаге нужно исключить влияние сезонной вариации. Воспользуемся методом скользящей средней. Заполним таблицу.
| Номер квартала | Объем продаж | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 4,75 | 5,5 | -1,5 | ||
| 6,25 | 6,5 | -1,5 | ||
| 6,75 | 7,125 | 2,875 | ||
| 7,5 | ||||
| 8,5 | 8,75 | -1,75 | ||
| 9,75 | -0,75 | |||
| 10,5 | 11,5 | 0,5 | ||
| 12,5 | ||||
1 год = 4 квартала. Поэтому найдем среднее значение объема продаж за 4 последовательных квартала. Для этого нужно сложить 4 последовательных числа из 2-го столбца, эту сумму разделить на 4 (количество слагаемых) и результат записать в 3-й столбец напротив третьего слагаемого.
(4 + 6 + 4 + 5)/4 = 4,75 (пишем напротив 4).
(6 + 4 + 5 + 10)/4 = 6,25 (пишем напротив 5). И т. д.
Полусумму двух соседних чисел из 3-го столбца запишем в 4-й столбец напротив верхнего из них. Если при заполнении 3-го столбца скользящая средняя вычислялась для нечетного числа сезонов, то результат записывается напротив среднего слагаемого и данные не надо центрировать (то есть не надо заполнять 4-й столбец). 5-й столбец – это разность 2-го и 4-го столбцов (2-го и 3-го столбцов, если скользящая средняя вычислялась для нечетного числа сезонов).
Заполним следующую таблицу. Оценки сезонной вариации запишем под соответствующим номером квартала в году. В каждом столбце вычисляем среднее = (сумма чисел в столбце)/(количество чисел в столбце). Результат пишем в строке «Среднее» (округления до одной цифры после запятой). Сумма чисел в строке «Среднее» равна – 1.
Скорректируем значения в строке «Среднее», чтобы общая сумма была равна 0. Это необходимо, чтобы усреднить значения сезонной вариации в целом за год.
Корректирующий фактор вычисляется следующим образом: сумма оценок сезонных вариаций (– 1) делится на число кварталов в году (4). Поэтому из каждого числа этой строки нужно вычесть – 1/4 = – 0,25. Так как у нас округления до одной цифры после запятой, то из нечетных столбцов вычтем – 0,3, а из четных столбцов вычтем – 0,2.
| Номер квартала в году | |||||
| -1,5 | -1,5 | ||||
| 2,875 | -1,75 | -0,75 | |||
| 0,5 | Сумма | ||||
| Среднее | 1,7 | 0,0 | -1,6 | -1,1 | -1 |
| Скорректированная сезонная вариация | 2,0 | 0,2 | -1,3 | -0,9 | 0,0 |
В последней строке получены значения сезонной вариации для соответствующего квартала года.
Исключим сезонную вариацию из фактических данных. Проведем десезонализацию данных.
| Номер квартала | Объем продаж A | Сезонная вариация S | Десезонализированный объем продаж A – S = T + E |
| 2 | |||
| 0,2 | 5,8 | ||
| -1,3 | 5,3 | ||
| -0,9 | 5,9 | ||
| 0,2 | 7,8 | ||
| -1,3 | 8,3 | ||
| -0,9 | 9,9 | ||
| 0,2 | 13,8 | ||
| -1,3 | 16,3 |
Из чисел 2-го столбца вычитаем числа 3-го столбца и результат пишем в 4-м столбце.
Уравнение линии тренда T = a + bx.
Найдем коэффициенты a и b по данным первого и последнего столбцов.
| Номер | x | y | x2 | xy |
| 5,8 | 11,6 | |||
| 5,3 | 15,9 | |||
| 5,9 | 23,6 | |||
| 7,8 | 46,8 | |||
| 8,3 | 58,1 | |||
| 9,9 | 79,2 | |||
| 13,8 | ||||
| 16,3 | 179,3 | |||
| Сумма | 93,1 | 684,5 |
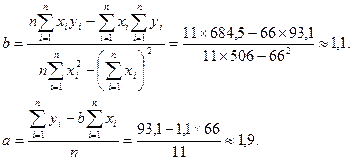
Замечание. Вместо вычислений коэффициентов a и b по формулам можно воспользоваться статистическими функциями ОТРЕЗОК (изв_знач_ y; изв_знач_ x) и НАКЛОН (изв_знач_ у; изв_знач_ х) мастера функций fx пакета Excel. Здесь изв_знач_ y и изв_знач_ x – это ссылки на ячейки, содержащие значения переменных y и x соответственно.
Трендовое значение объема продаж = 1,9 + 1,1×(номер квартала). Теперь займемся расчетом ошибок.
| Номер квартала | Объем продаж A | Десезонализирован-ный объем продаж A – S = T + E | Трендовое значение | Ошибка еt | | еt | | еt 2 |
| 2 | -1 | |||||
| 5,8 | 4,1 | 1,7 | 1,7 | 2,89 | ||
| 5,3 | 5,2 | 0,1 | 0,1 | 0,01 | ||
| 5,9 | 6,3 | -0,4 | 0,4 | 0,16 | ||
| 7,4 | 0,6 | 0,6 | 0,36 | |||
| 7,8 | 8,5 | -0,7 | 0,7 | 0,49 | ||
| 8,3 | 9,6 | -1,3 | 1,3 | 1,69 | ||
| 9,9 | 10,7 | -0,8 | 0,8 | 0,64 | ||
| 11,8 | -1,8 | 1,8 | 3,24 | |||
| 13,8 | 12,9 | 0,9 | 0,9 | 0,81 | ||
| 16,3 | 2,3 | 2,3 | 5,29 | |||
| Сумма | 11,6 | 16,58 |
Из чисел 3-го столбца приводимой выше таблицы вычитаем числа 4-го столбца и результат пишем в 5-м столбце.
Среднее абсолютное отклонение MAD = ∑│et│/ n = 11,6/11 ≈ 1,1, среднеквадратическая ошибка MSE = ∑│et2│/ n = 16,58/11 ≈ 1,5. Мы видим, что ошибки достаточно велики. Это скажется на качестве прогноза.
Дадим прогноз объема продаж на следующие два квартала.
Мы считаем, что тенденция, выявленная по прошлым данным, сохранится и в ближайшем будущем. Подставляем номера кварталов в формулу и учитываем сезонную вариацию.
Прогноз объема продаж в 12-м квартале:
(1,9 + 1,1×12) + (–0,9) = 14,2 тыс. руб.
Прогноз объема продаж в 13-м квартале:
(1,9 + 1,1×13) + 2 = 18,2 тыс. руб.
 2015-05-18
2015-05-18 1448
1448








