Мультиколлинеарность – это взаимная зависимость влияющих переменных. Проблема состоит в том, что при её наличии становится сложно или невозможно разделить влияние регрессоров на зависимую переменную, и коэффициенты теряют экономический смысл предельной функции или эластичности. Дисперсии коэффициентов растут, сами коэффициенты, оценённые по различным выборкам или методом Монте-Карло, коррелируют между собой. Это приводит к тому, что в области настройки модели графики Y и Y^ прекрасно совпадают, R2 и F высокие, а в области прогноза графики могут совпасть, как на Рисунке 7.5.2, что можно объяснить взаимным подавлением погрешностей (см. стр. ….), или расходятся, как на Рисунке 7.5.1, то есть модель оказывается неадекватной.
Как обнаружить мультиколлинеарность? Проще всего – по корреляционной матрице. Если коэффициенты корреляции регрессоров больше 0,7, значит, они взаимосвязаны. Числовой характеристикой мультиколлинеарности может служить определитель корреляционной матрицы. Если он близок к 1, то регрессоры независимы; если к 0, значит они связаны сильно.
Как бороться с мультиколлинеарностью?
1. Смириться, принять во внимание и ничего не делать.
2. Увеличить объём выборки: дисперсии коэффициентов обратно пропорциональны количеству замеров.
3. Удалять из модели регрессоры, слабо коррелирующие с зависимой переменной, или коэффициенты которых имеют малую t-статистику. Как видно из таблицы 7.10, при этом происходит смещение коэффициентов при значимых регрессорах, и возникает вопрос об их экономическом смысле. F -статистика, то есть качество модели, при этом растёт.
4. Использовать в уравнении регрессии агрегаты из коррелирующих переменных: линейные комбинации с коэффициентами, обратно пропорциональными стандартным отклонениям переменных и выравнивающими их масштабы. Такие агрегаты обычно не имеют экономического смысла, но могут повысить адекватность модели.
5. Факторный анализ, или Метод главных компонент. Используется, если переменных много, но они являются линейными комбинациями небольшого количества независимых факторов, может быть, не имеющих экономического смысла. На Рисунке … приведён пример: имеется три ортогональных вектора Z1, Z2, Z3 и пять векторов X1, X2, X3, X4, X5, которые можно представить как линейные комбинации из Z1, Z2, Z3.
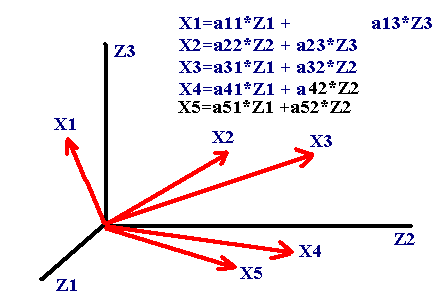
Рис.7.6. Представление векторов Х через ортогональные векторы Z.
 2015-05-18
2015-05-18 2316
2316








