Модель авторегрессии порядка p – АР(p) имеет вид
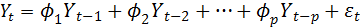
(4.8.8)
Для компактного описания этого процесса введем понятие оператора сдвига назад B: 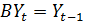 ;
; 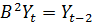 ; ….
; …. 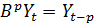 .
.
Тогда математическая модель может быть записана в следующем виде
 (4.8.9)
(4.8.9)
где 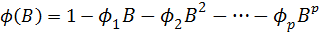 . (4.8.10)
. (4.8.10)
Процесс авторегрессии не всегда стационарен. Вопрос о стационарности процесса авторегрессии можно выяснить с помощью так называемого характеристического уравнения
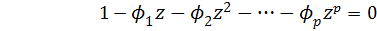 (4.8.11)
(4.8.11)
Если все комплексные корни характеристического уравнения лежат вне единичного круга, то есть 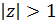 , то процесс авторегрессии является стационарным. Отметим, что данное требование является обязательным.
, то процесс авторегрессии является стационарным. Отметим, что данное требование является обязательным.
Пример. Процесс авторегрессии первого порядка 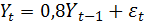 имеет характеристическое уравнение
имеет характеристическое уравнение 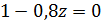 с корнем
с корнем 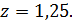 Так как
Так как 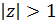 , то процесс стационарен. Его значения колеблются вокруг нуля.
, то процесс стационарен. Его значения колеблются вокруг нуля.
Процесс авторегрессии первого порядка 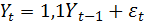 имеет характеристическое уравнение
имеет характеристическое уравнение 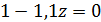 с корнем
с корнем 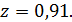 Так как
Так как 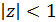 , то процесс не стационарен. Коэффициент 1,1 приводит к постоянному увеличению последующих значений процесса.
, то процесс не стационарен. Коэффициент 1,1 приводит к постоянному увеличению последующих значений процесса.
Для процесса авторегрессии диагностической функцией ее порядка является так называемая частная автокорреляционная функция (ЧАК).
Предположим, что 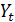 описывается процессом авторегрессии порядка τ
описывается процессом авторегрессии порядка τ
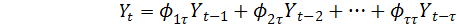 (4.8.12)
(4.8.12)
При этом последний коэффициент 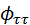 называется коэффициентом частной автокорреляции для величины лага τ.
называется коэффициентом частной автокорреляции для величины лага τ.
Ряд ЧАК(τ) называется частной актокорреляционной функцией. Для процесса АР(p) ЧАК(τ)=0 для значений 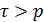 .
.
 2015-05-18
2015-05-18 708
708








