Рассмотрим ряд частных моделей Бокса-Дженкинса для стационарного процесса 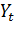 c нулевым математическим ожиданием. Если математическое ожидание процесса не равно нулю (
c нулевым математическим ожиданием. Если математическое ожидание процесса не равно нулю (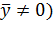 , то вычитая это значение из всех значений временного ряда, можно получить временной ряд с нулевым математическим ожиданием.
, то вычитая это значение из всех значений временного ряда, можно получить временной ряд с нулевым математическим ожиданием.
А) Модель скользящего среднего 1-го порядка СС(1)
Модель скользящего среднего 1-го порядка имеет вид
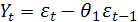
(4.8.5)
где 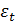 - некоррелированная случайная величина с
- некоррелированная случайная величина с
нулевым математическим
ожиданием (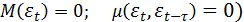 и постоянной
и постоянной
дисперсией (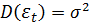 );
);
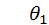 – параметр модели.
– параметр модели.
Нетрудно видеть, что процесс СС(1) обладает следующими свойствами:
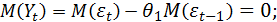
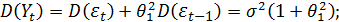
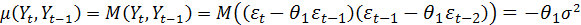
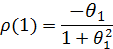
При 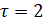
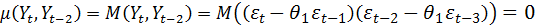
Аналогично при всех остальных τ (2,3,…) 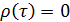 .
.
Б) Модель скользящего среднего q-го порядка СС(q)
Модель скользящего среднего q -го порядка имеет вид
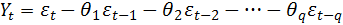
(4.8.6)
Процесс СС(q)обладает следующими свойствами
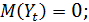
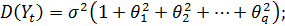
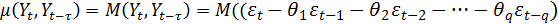
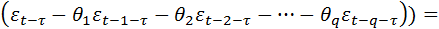
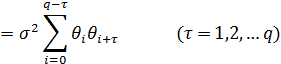
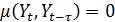 при
при 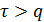 .
.
 2015-05-18
2015-05-18 578
578








