Линейная модель множественной регрессии. Обобщением парной линейной регрессионной модели является линейная регрессионная модель с m объясняющими переменными (линейная модель множественной

Обобщением парной линейной регрессионной модели является линейная регрессионная модель с m объясняющими переменными (линейная модель множественной регрессии):

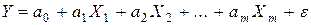. (3.2)

Здесь a = (a ₀, a ₁, …, a_m) – вектор неизвестных параметров размерности (m + 1).

Величина a_j (j = 1, 2, …, m)называется j -м теоретическим коэффициентом регрессии. Он характеризует чувствительность величины Y к изменению X_j. Другими словами, коэффициент регрессии a_j отражает влияние на функцию регрессии

y = a ₀ + a ₁ x ₁ + a ₂ x ₂ + … + a_mx_m (3.3)

объясняющей переменной X_j при условии, что все другие объясняющие переменные модели остаются постоянными: он показывает, на сколько единиц изменяется среднее значение результирующей переменной Y при увеличении объясняющей переменной X_j на одну единицу своего измерения. Величина a ₀ – свободный член, определяющий значение функции регрессии (3.3), когда все объясняющие переменные равны нулю (если, конечно, это имеет смысл в рамках модели).

После выбора линейной функции в качестве модели зависимости рассматриваемых переменных необходимо оценить параметры этой модели.

Предположим, что проведено n наблюдений над объясняющими переменными X ₁, X ₂, …, X_m и зависимой переменной Y. Обозначим i -е значение зависимой переменной y_i, а объясняющих переменных – 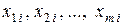. Тогда для каждого наблюдения будет иметь место зависимость вида

y_i = a ₀ + a ₁ × x _{1 i} + a ₂ × x _{2 i} + …. + a_m× x_{m i} + e _i, (3.4)

где e _i – случайное возмущение i -го наблюдения, i = 1, 2, …, n.

Представим данные наблюдений и соответствующие коэффициенты в матричной форме:

, .

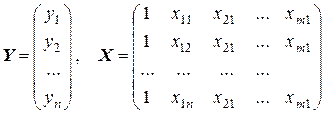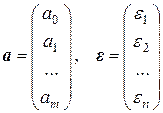Здесь Y – n -мерный вектор-столбец значений зависимой переменной Y;

X – матрица размерности n ´ (m + 1), в которой (j + 1)-й столбец (j = 1, 2, …, m) представляет результаты наблюдений независимой переменной X_j (единичный столбец соответствует переменной при свободном члене a ₀);

а – вектор-столбец размерности (m + 1) параметров модели;

e – вектор-столбец размерности n случайных возмущений (отклонений).

Тогда в матричной форме модель (3.4) примет вид:

Y = X × a + e. (3.5)

Как и в случае парной регрессии, истинные значения параметров a _j (j = 0, 1, 2, …, m) по выборке получить невозможно, их можно только оценить. Поэтому определяются коэффициенты 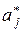(j = 0, 1, 2, …, m) так называемого выборочного уравнения множественной регрессии:

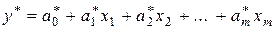, (3.6)

где 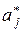– оценка неизвестного параметра a _j (j = 0, 1, 2, …, m).

Самым распространенным методом нахождения оценок параметров множественной линейной регрессии является метод наименьших квадратов (МНК). Напомним, что его суть состоит в минимизации суммы квадратов отклонений e_i наблюдаемых значений y_i зависимой переменной Y от значений 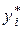(i = 1, 2, …, n), получаемых по уравнению регрессии (3.6). Эти отклонения рассчитываются, очевидно, по формуле

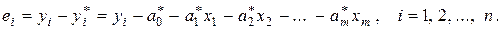(3.7)

Согласно МНК, для нахождения оценок 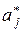(j = 0, 1, 2, …, m) минимизируется функция

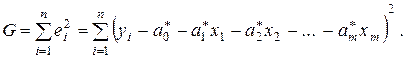
Необходимым условием минимума функции G является равенство нулю всех ее частных производных по 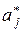(j = 0, 1, 2, …, m). Произведя необходимые вычисления и преобразования, получаем систему нормальных уравнений из

(m + 1) линейных уравнений с (m + 1) неизвестными:

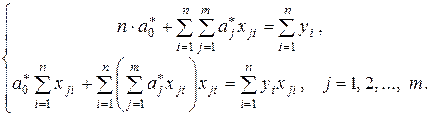(3.8)

Запишем систему (3.8) в матричной форме:

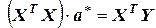. (3.9)

Здесь X ^T – матрица, транспонированная к X;

a ^* – вектор-столбец размерности (m + 1) оценок 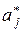(j = 0, 1, 2, …, m)

параметров модели;

Y – вектор-столбец размерности n значений зависимой переменной Y.

Для решения матричного уравнения (3.9) относительно вектора оценок a ^* необходимо ввести следующую предпосылку 6 ⁰ (см. п. 2.3, тема 2) для множественного регрессионного анализа:

6 ⁰. Векторы-столбцы матрицы X являются линейно независимыми, т.е.

ранг матрицы X равен (m + 1) – числу неизвестных

параметров: rang (X) = m + 1.

Кроме того, предполагается, что число имеющихся наблюдений n больше числа неизвестных параметров, т.е. n > m + 1, ибо в противном случае в принципе невозможно получение сколь-нибудь надежных статистических выводов.

Из предположения 6 ⁰ следует, что ранг симметричной матрицы X ^T X, который совпадает с рангом матрицы X, равен ее порядку, т.е. rang (X ^T X) =

m + 1. Из матричной алгебры известно, что в этом случае матрица X ^T X является невырожденной, т.е. ее определитель не равен нулю. Следовательно, существует матрица (X ^T X)^{– 1}, обратная к матрице X ^T X.

Умножая слева уравнение (3.9) на матрицу (X ^T X)^{– 1}, получаем

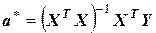. (3.10)

Зная вектор а ^*, выборочное уравнение множественной регрессии можно записать в виде:

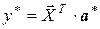, (3.11)

где – вектор-строка значений объясняющих переменных X ₁,…, X_m (первая координата, равная единице, соответствует свободному члену).

Пример 3.1. Имеются следующие данные о сменной добыче угля на одного рабочего Y (т), мощности пласта X ₁(м) и уровне механизации работ X ₂ (%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 3.1

i	x 1 i	x 2 i	yi	i	x 1 i	x 2 i	yi

Предполагая, что между переменными Y, X ₁ и X ₂ существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y на X ₁ и X ₂).

Решение. Обозначим

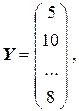
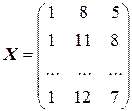
(напомним, что в матрицу X вводится дополнительный столбец чисел, состоящий из единиц). Тогда

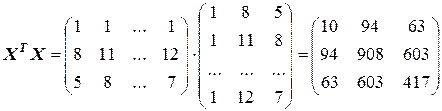
и

.

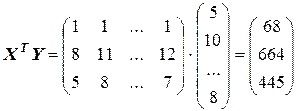Матрицу A ^{– 1} = (X ^T X)^{– 1} определим по формул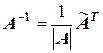е , где 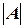– определитель матрицы 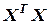; 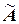– матрица, присоединенная к матрице .

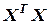Найдем определитель 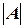= 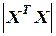, разложив его по элементам первой строки:

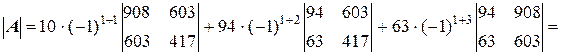
= 10×15027 – 94×1209 + 63×(– 522) = 3 738.

Вычислим алгебраические дополнения 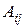каждого элемента a_ij матрицы A по формуле:

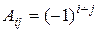D _ij,

где D _ij – определитель матрицы, полученной из матрицы A вычеркиванием i -й строки и j -го столбца. Например,

; ;

.

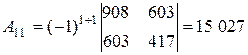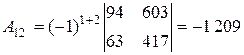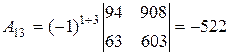Составляем присоединенную матрицу

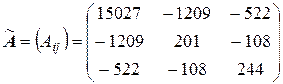
и транспонируем ее:

.

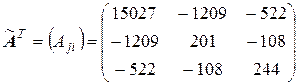Отметим, что 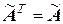, так как матрица 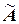симметричная.

Наконец, получаем

A ^{– 1} = (X ^T X)^{– 1} = .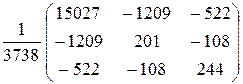

В соответствии с формулой (3.10), умножая эту матрицу на вектор 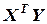, находим

.

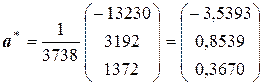С учетом (3.6) выборочное уравнение множественной регрессии имеет вид:

y ^* = – 3,54 + 0,854 x ₁ + 0,367 x ₂.

Оно показывает, что при увеличении только мощности пласта на 1 м (при неизменном уровне механизации работ) добыча угля на одного рабочего увеличится в среднем на 0,854 т, а при увеличении только уровня механизации работ на 1% (при неизменной мощности пласта) – в среднем на 0,367 т. g