Свойства МНК-оценок

Приведенные ранее (см. п. 2.3, тема 2) предпосылки 1 ⁰ – 5 ⁰ для парного регрессионного анализа и, кроме того, предпосылка 6 ⁰ о невырожденности матрицы значений объясняющих переменных для множественного регрессионного анализа могут быть записаны следующим образом:

1 ⁰. В модели (3.5) e – случайный вектор, а X – неслучайная (детерминированная) матрица.

2 ⁰. M (e) = 0, где 0 – нулевой вектор размера n.

3 ⁰, 4 ⁰. Ковариационная матрица вектора возмущений e

K (e) = M (e^Te) =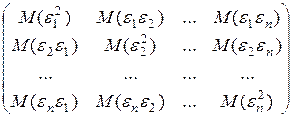

представима в виде

K (e) = s ² E,

где E – единичная матрица n -го порядка.

5 ⁰. Вектор возмущений e – нормально распределенный случайный вектор, т.е. e ~ N (0, s E).

6 ⁰. rang (X) = m + 1 < n.

МНК-оценки (3.10) для модели (3.5) множественной линейной регрессии обладают свойствами, аналогичным свойствам МНК-оценок для парной линейной модели. Другими словами, теорема Гаусса – Маркова, рассмотренная выше для парной регрессионной модели (см. п. 2.3, тема 2), оказывается верной и в общем виде для модели (3.5) множественной регрессии.

Теорема 3.1 (Гаусса – Маркова). Если выполнены предпосылки 1 ⁰ – 4 ⁰ и

6 ⁰, то вектор МНК-оценок a ^* обладает следующими свойствами:

· оценки являются несмещенными, т.е. M (a ^*) = a;

· D (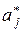) = s ² × z_j, (3.12)

гдеz_j = z_jj – элемент матрицы 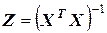, стоящий на пересеченииj-

й строки иj-го столбца ( j = 0, 1, …, m );

· оценки состоятельны: a ^* ® a по вероятности при n ® ¥;

· оценки эффективны, т.е. они имеют наименьшие дисперсии по сравнению с любыми другими несмещенными оценками, линейными относительно величин y_i, i = 1, 2, …, n.

Несмещенной оценкой дисперсии «возмущений» (остаточной дисперсии) s ² является выборочная остаточная дисперсия

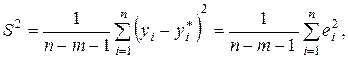(3.13)

где

m – количество объясняющих переменных модели;

y_i ^* – значение зависимой переменной Y, найденное по выборочному

уравнению регрессии (3.6);

e_i = y_i – y_i ^* – выборочная оценка возмущения e _i, или остаток регрессии.

Оценками дисперсий выборочных коэффициентов регрессии, в силу (3.12), являются величины

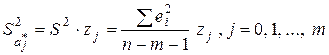. (3.14)

Как и в случае парной регрессии, величина 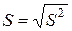часто называется стандартной ошибкой регрессии, а 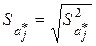– стандартной ошибкой j–го коэффициента регрессии.

Пример 3.2. По данным примера 3.1 вычислить выборочную остаточную дисперсию и стандартные ошибки коэффициентов регрессии.

Решение. Для вычисления выборочной остаточной дисперсии S ² составим следующую таблицу:

Таблица 3.2

i	x 1 i	x 2 i	yi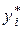
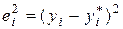
				5,13	0,016
				8,79	1,464
				9,64	1,127
				5,98	1,038
				5,86	0,741
				6,23	0,052
				6,35	0,121
				5,61	0,377
				5,13	0,762
				9,28	1,631
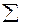
				–	6,329

По формуле (3.13) определяем, что

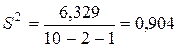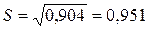и (т).

Из найденной в примере 3.1 матрицы 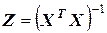видно, что

.

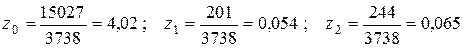Следовательно, в силу (3.14) выборочные дисперсии и стандартные ошибки коэффициентов регрессии равны:

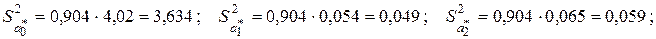
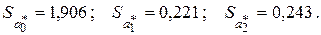g