Коэффициент корреляции и проверка его значимости

Одним из важнейших элементов эконометрического анализа является установление наличия и тесноты связи между различными показателями (например, между ценой и спросом, доходом и потреблением, инфляцией и безработицей). Обычно анализ начинают с простейшей – линейной зависимости.

Числовой характеристикой, измеряющей степень тесноты линейной статистической связи между случайными переменными Х и Y, является коэффициент корреляции между Х и Y, который обозначается r = 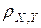и определяется по формуле

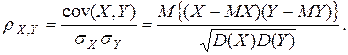
Приведем основные его свойства.

1. Для любых переменных Х и Y абсолютная величина коэффициента корреляции не превосходит единицы: 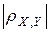£ 1, или – 1 £ 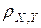£ + 1.

2. Абсолютная величина коэффициента корреляции равна единице тогда и только тогда, когда между переменными Х и Y существует линейная функциональная зависимость, т. е. Y = aX + b, где a ¹ 0 и b – некоторые постоянные величины. При этом 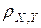= 1, если a > 0, и 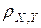= – 1, если a < 0.

3. Если переменные Х и Y независимы, то коэффициент корреляции между ними равен нулю. Обратное утверждение (из равенства нулю коэффициента корреляции между Х и Y следует их независимость) верно лишь для некоторых частных случаев и неверно в общем случае. В том случае, когда 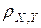= 0, говорят, что переменные Х и Y некоррелированные; в противном случае они коррелированные.

Из этих свойств вытекает смысл 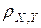, который состоит в том, что коэффициент корреляции характеризует тесноту линейной статистической связи между переменными Х и Y: чем ближе 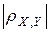к единице, тем связь сильнее; чем ближе 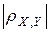к нулю, тем связь слабее. Переменные X и Y называются положительно коррелированными, если 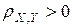и отрицательно коррелированными, если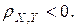

Определение и свойства теоретического коэффициента корреляции 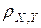показывают, что изучение линейной статистической зависимости между переменными Х и Y имеет смысл лишь тогда, когда величина r =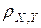 значима (или существенна), т. е. не очень близка к нулю. Однако эта величина на практике, как правило, неизвестна и может быть лишь оценена с помощью выборочных данных.

Точечной оценкой теоретического коэффициента корреляции 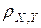является выборочный коэффициент корреляции r = r_xy, который находится по формуле

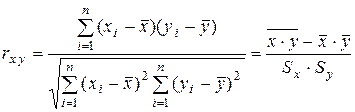. (2.33)

В формуле (2.33)

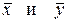– выборочные средние переменных X и Y соответственно;

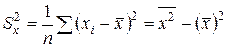– выборочная дисперсия переменной X;

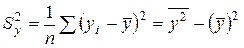– выборочная дисперсия переменной Y;

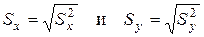– выборочные среднеквадратические (стандартные) отклонения переменных X и Y соответственно;

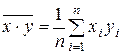– выборочное среднее переменной X× Y.

Исходя из определения (2.33), можно показать, что выборочный коэффициент корреляции также обладает сформулированными выше свойствами 1 – 3.

Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между переменными, полученное по выборочным данным, в известной мере может быть распространено и на генеральную совокупность. Для достижения этой цели используется критерий, основанный на распределении Стьюдента.

Пусть основная гипотеза Н₀состоит в том, что корреляция между Х и Y не значима, т. е. Н₀: 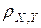= 0. Альтернативная гипотеза Н₁= 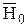состоит в том, что корреляция между Х и Y значима. Если справедлива нулевая гипотеза Н₀ и объем выборки n достаточно велик, то статистика

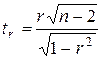(2.34)

имеет приближенно распределение Стьюдента с (n – 2) степенями свободы.

Для заданного уровня значимости a находим по таблице 1 Приложения

t _1–a/2(n – 2) – квантиль порядка (1– a /2) распределения Стьюдента с (n – 2) степенями свободы. Тогда нулевая гипотеза Н₀принимается при выполнении неравенства

| t_r | < t _1–a/2(n – 2).

В противном случае гипотеза Н₀отклоняется в пользу альтернативной Н₁.

Если гипотеза H₀ отклоняется, то это означает, что коэффициент корреляции между ними значим. Следовательно, переменные Х и Y коррелированны, и можно изучать линейную зависимость между ними.

Замечание 2.4. Для оценки значимости коэффициента корреляции на начальном этапе исследования можно воспользоваться следующей грубой оценкой:

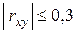· – линейная связь отсутствует;

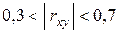· – имеется слабая линейная связь;

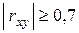· – имеется сильная линейная связь. 3

Пример 2.6. По данным примера 2.2 вычислить коэффициент корреляции между переменными Х и Y. Значима ли зависимость между Х и Y? Проверить гипотезу на уровне значимости 0,01.

Решение. В примере 2.2 были определены

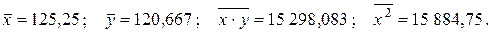
Вычислим далее среднее

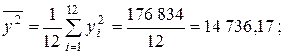
дисперсии

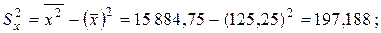
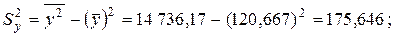
стандартные отклонения

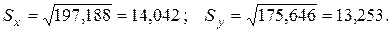
По формуле (2.33) находим

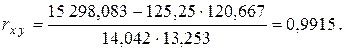
Данное значение коэффициента корреляции позволяет сделать вывод о сильной (прямой) линейной статистической зависимости между рассматриваемыми переменными Х и Y.

Проверим гипотезу Н₀: 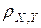= 0 против альтернативной Н₁: 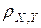¹ 0 на уровне значимости a = 0,01. По формуле (2.34) вычислим статистику

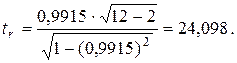
С помощью таблицы квантилей распределения Стьюдента определим

t _1–a/2(n – 2) = t _{0, 995}(10) = 3,1693. Поскольку | t_r | > t _1–a/2(n – 2) (24,098 > 3,1693), то коэффициент корреляции r_{x y} статистически значим. Следовательно, 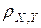существенно отличается от нуля и между переменными Х и Y существует сильная линейная статистическая зависимость. g

Замечание 2.5. Сравнивая формулы (2.7) и (2.33) для коэффициентов регрессии и корреляции соответственно, нетрудно заметить, что в линейной модели между ними существует зависимость:

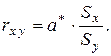
Так, используя результаты вычислений в примерах 2.2 и 2.6, получаем

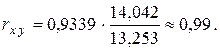
Некоторое (незначительное) расхождение с величиной, полученной в примере 2.6, вызвано ошибками округлений. 3

Замечание 2.6. В случае парной линейной регрессионной модели квадрат коэффициента корреляции между зависимой и независимой переменной равен коэффициенту детерминации:

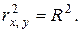
Так для данных примера 2.2 R ² = 0,983» (0,9915)² = 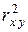(см. примеры 2.5 и 2.6); неточности в данном случае связаны с округлением вычислений. 3

Контрольные вопросы

1. Что такое функция регрессии?

2. Чем регрессионная модель отличается от функции регрессии?

3. Какая регрессионная модель называется линейной?

4. Какой смысл имеют коэффициенты парного линейного уравнения регрессии?

5. В чем состоит различие между теоретическим и выборочным уравнением регрессии?

6. В чем сущность метода наименьших квадратов (МНК)?

7. Приведите формулы расчета коэффициентов парного линейного уравнения регрессии по МНК.

8. Перечислите предпосылки регрессионного анализа.

9. Сформулируйте основные свойства МНК-оценок.

10. Имеют ли коэффициенты парной линейной регрессии размерность?

11. Как оценивается дисперсия возмущений?

12. Какие факторы влияют на величину стандартных ошибок коэффициентов регрессии?

13. Как строятся интервальные оценки коэффициентов регрессии?

14. Как строятся доверительные полосы для: а) уравнения регрессии; б) индивидуальных значений результирующей переменной?

13. Какие виды прогнозов Вы знаете?

14. В чем суть предсказания: а) среднего значения; б) индивидуальных значений результирующей переменной?

15. Объясните суть коэффициента корреляции.

16. Сформулируйте основные свойства коэффициента корреляции.

17. Почему коэффициент корреляции называют мерой линейной зависимости между переменными?

18. В чем суть значимости коэффициента корреляции и как она проверяется?

19. Опишите «грубое» правило анализа статистической значимости коэффициента корреляции.

20. Как связаны коэффициенты регрессии и корреляции в парной регрессионной линейной модели?

21. В чем суть статистической значимости коэффициентов регрессии? Как она проверяется?

22. Опишите «грубое» правило анализа статистической значимости коэффициентов регрессии.

23. Объясните суть коэффициента детерминации.

24. В чем суть статистической значимости уравнения регрессии? Как она проверяется?

25. Как связаны коэффициенты детерминации и корреляции в парной регрессионной линейной модели?