Нелинейные модели регрессии и их линеаризация

Различают два класса нелинейных моделей регрессии:

· регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по параметрам;

· регрессии, нелинейные по параметрам.

Примерами нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

· полиномы разных степеней –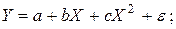

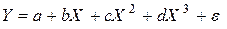и т.д.

· равносторонняя гипербола – .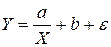

Для оценки параметров нелинейных моделей используются два подхода.

Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризирующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.

В рамках первого подхода можно линеаризировать модели как нелинейные по переменным, так и нелинейные по параметрам.

Если модель нелинейна по переменным, но линейна по параметрам, то введением новых переменных ее можно свести к линейной модели и для оценки параметров новой модели использовать обычный метод наименьших квадратов.

Среди подобных моделей следует назвать хорошо известную в эконометрике обратную (или гиперболическую) регрессионную модель

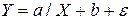. (4.1)

Модель (4.1) может быть использована в микроэкономике для описания связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товара с величиной товарооборота и т.п. Модели вида (4.1) находят применение и в макроэкономике. Классическим ее примером является модель Филлипса, характеризующая соотношение между нормой безработицы X и процентом прироста безработицы Y.

Введение в модели (4.1) новой переменной 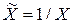, сводит ее к линейной:

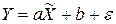. (4.2)

Параметры модели (4.2) оцениваются обычным методом наименьших квадратов по формулам (2.7) и (2.8) (тема 2), где данные x_i заменяются на 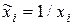, i = 1, 2, …, n.

Другим примером нелинейных зависимостей может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов или доходов. Математическое описание подобного рода взаимосвязей получило название моделей Энгеля. На основе исследования семейных расходов Энгель сформулировал следующее утверждение: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается; соответственно с увеличением дохода доля доходов, расходуемых на непродовольственные товары, будет возрастать. Однако это увеличение не беспредельно, так как сумма долей на все товары не может быть больше единицы.

Оказалось, что гиперболическая модель (4.1) с параметром a < 0 хорошо подходит для описания подобной зависимости. Вместе с тем равносторонняя гипербола не является единственно возможной функцией регрессии для модели Энгеля. Для этой цели можно использовать также полулогарифмическую модель

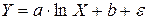. (4.3)

Данная модель линейна по параметрам a и b и нелинейна по независимой переменной X, однако введением новой переменной 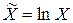она приводится к линейной:

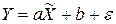. (4.4)

Пример 4.1. Имеются данные о среднемесячном доходе семьи X (в тыс. усл. ед.) и расходах на товары длительного пользования Y (в % к доходам):

Таблица 4.1

Номер семьи
X
Y		13,4	15,4	16,5	18,6,	19,1

Найти уравнение регрессии Y на X:

а) полулогарифмическое; б) гиперболическое. Представить их графически.

Решение. а). Вводим новую переменную 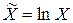и вычисляем необходимые средние для расчета функции регрессии:

.

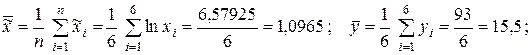
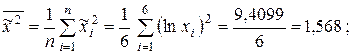
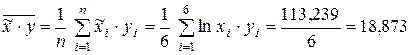Формулы (2.7) и (2.8) (тема 2) дают нам следующие оценки параметров функции регрессии:

.

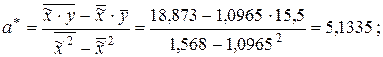
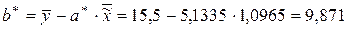Таким образом, полулогарифмическая функция Энгеля регрессии доли расходов на товары длительного пользования на среднемесячные доходы семьи имеет вид: y ^* = 9,871 + 5,1335× ln x.

График этой функции изображен на рис. 4.1 сплошной линией.

б). Вводим новую переменную 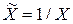и вычисляем необходимые средние:

.

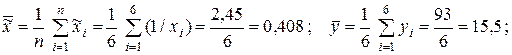
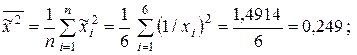
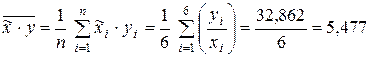Применение формул (2.7) и (2.8) (тема 2) дает следующие оценки параметров функции регрессии:

.

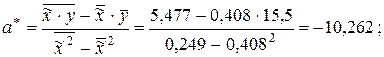
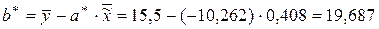Следовательно, гиперболическая функция Энгеля регрессии доли расходов на товары длительного пользования на среднемесячные доходы семьи имеет вид:

.

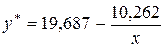График данной функции представлен на рис. 4.1 разрывной линией.

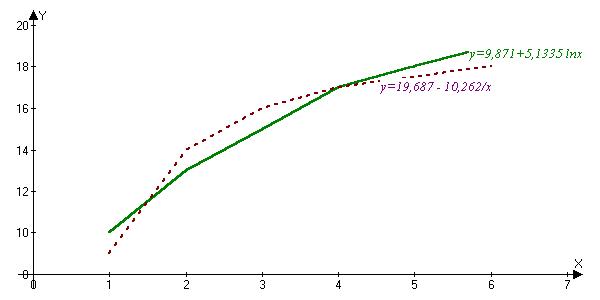
Рис. 4.1. Нелинейные функции регрессии g

Более сложной проблемой оценивания являются модели нелинейные по параметрам, так как непосредственное применение метода наименьших квадратов для оценки параметров таких моделей приводит, как правило, к значительным затруднениям. Примерами подобных нелинейных регрессий могут служить модели, функции регрессий которых есть функции:

· степенная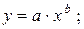

· показательная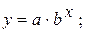

· экспоненциальная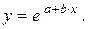

В ряде случаев с помощью подходящих преобразований эти модели удается cвести к линейным. Так, приведенные выше модели могут быть сведены к линейным логарифмированием обеих частей уравнений.