2015-05-18
523
Как и в парной регрессии, одной из важнейших задач множественного регрессионного анализа является прогнозирование развития изучаемого явления на основе построенной модели. При этом можно рассматривать как точечный, таки интервальный прогноз значений результирующей переменной Y.
Пусть требуется оценить прогнозное среднее значение результирующей переменной Y для заданного вектора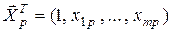 
значений объясняющих переменных X 1, X 2, …, Xm.
Точечный прогноз среднего значения результирующей переменной Y рассчитывается по выборочному уравнению регрессии:
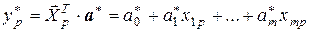. (3.23)
Интервальный прогноз среднего значения результирующей переменной Y для заданного вектора 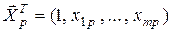значений объясняющих переменных X 1, X 2, …, Xm определяется доверительным интервалом (3.17) при 
:
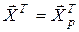прогнозируемое среднее значение результирующей переменной Y с надежностью (доверительной вероятностью) g = 1 – a накрывается интервалом с границами
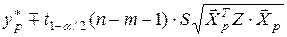, (3.24)
где yp * – точечный прогноз среднего значения Y.
Интервальный прогноз индивидуального значения результирующей переменной Y для заданного вектора 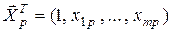значений объясняющих переменных X 1, X 2, …, Xm определяется доверительным интервалом (3.18) при :
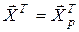прогнозируемое значение результирующей переменной Y с надежностью (доверительной вероятностью) g = 1 – a принадлежит интервалу с границами
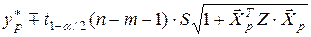, (3.25)
где yp * – точечный прогноз среднего значения Y.
Пример 3.4. По данным примера 3.1 необходимо:
1) построить 95%-е доверительные интервалы для коэффициентов регрессии и остаточной дисперсии;
2) оценить сменную добычу угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6%;
3) спрогнозировать с надежностью 0,95 среднее и индивидуальное значения сменной добычи угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6%.
Решение. 1). С помощью табл. 1 Приложения при числе степеней свободы n – m – 1 = 10 – 2 – 1 = 7 и порядке 1 – a /2 = 1 – 0,05/2 = 0,975 находим t 0, 975 (7) = 2,3646. По формуле (3.15), учитывая результаты примеров 3.1 и 3.2, определяем 95%-е доверительные интервалы для теоретических коэффициентов множественной регрессии:
– 3,5393 – 2,3646×1,906 < a 0 < – 3,5393 + 2,3646×1,906;
0,8539 – 2,3646×0,221 < a 1 < 0,8539 + 2,3646×0,221;
0,3670 – 2,3646×0,243 < a 2 < 0,3670 + 2,3646×0,243,
или
– 8,0462 < a 0 < 0,9676;
0,3313 < a 1 < 1,3765;
– 0,2105 < a 2 < 0,9416.
По табл. 2 Приложения находим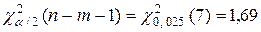 
и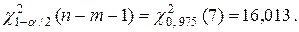 
Учитывая результат примера 3.2, по формуле (3.16) получаем:
,
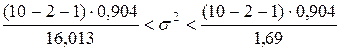или
0,3952 < s 2 < 3,7444 и 0,6286 < s < 1,9350.
2). По условию надо оценить среднее значение зависимой переменной Y при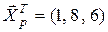 
. В силу (3.23) и результатов примера 3.1 находим:
= – 3,5391 + 0,8539×8 + 0,367×6 = 5,494 (т).
3). Для построения доверительных интервалов для среднего и индивидуального значений зависимой переменной Y найдем сначала величину
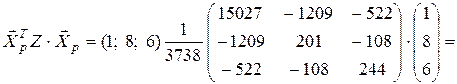
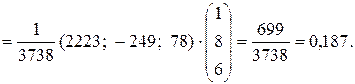
Теперь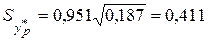 
(т) и 
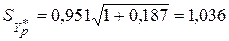(т).
Поскольку 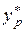= 5,494 и t 1 – a /2 (n – m – 1) = t 0, 975 (7) = 2,3646, по формулам (3.24) и (3.25) найдем:
5,494 – 2,3646×0,411 < yp < 5,494 – 2,3646×0,411;
5,494 – 2,3646×1,036 < Yp < 5,494 – 2,3646×1,036,
или
4,522 < yp < 6,466 (т);
3,044 < Yp < 7,944 (т).
Итак, средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6% с надежностью 0,95 «накрывается» доверительным интервалом (4,522; 6,466) (т), а соответствующее индивидуальное значение находится в пределах от 3,044 до 7,944 (т). g
