Проверить значимость уравнения регрессии – значить установить, соответствует ли математическая модель, выражающая зависимость между переменными,
TSS = RSS + ESS, (если МНК, в общем случае неверно),
где 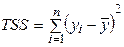 – общая сумма квадратов отклонений зависимой переменой y от ее среднего значения;
– общая сумма квадратов отклонений зависимой переменой y от ее среднего значения;
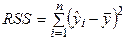 – сумма квадратов, обусловленная регрессией;
– сумма квадратов, обусловленная регрессией;
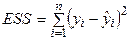 – остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
– остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
Часть дисперсии, объясненная регрессией 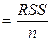
Часть дисперсии, необъясненная регрессией 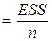
Дисперсия 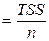 =
= 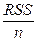 +
+ 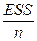
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии является коэффициент детерминации, определяемой по формуле
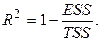 Причем
Причем 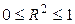 .
.
Коэффициент детерминации 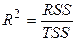 , если МНК
, если МНК
Коэффициент детерминации, определяемой по формуле
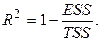 Причем
Причем 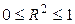 .
.
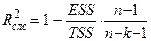
Чем ближе 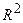 к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии.
к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии.
В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т.е.
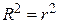 .
.
Мультиколинеарность – высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах.
Мультиколинеарность – этопочти линейная зависимость между значениями факторных переменных.
Признаки мультиколлинерности:
1) Небольшие изменения в исходных данных приводят к значительным изменениям оценок коэффициентов модели.
2) Оценки коэффициентов имеют большие стандартные ошибки, t- статистики для большинства коэффициентов модели малы (соответствующие факторы незначимы), в то время как F- статистика и коэффициент детерминации 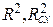 имеют высокие значения (модель в целом значима).
имеют высокие значения (модель в целом значима).
3) Оценки коэффициентов имеют неоправданно большие значения или неправильные знаки с точки зрения экономической теории.
4) Определить 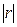 симметрической матрицы r, составленной из парных коэффициентов корреляции
симметрической матрицы r, составленной из парных коэффициентов корреляции 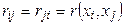 близок к «0».
близок к «0».
 2015-05-18
2015-05-18 551
551








