Молекулярно-кинетическое истолкование температуры и давления

Основное уравнение молекулярно-кинетической теории газов связывает параметры состояния газа (P и Т) с характеристиками поступательного движения его молекул.

Стенки сосуда, в котором заключен газ, подвергаются непрерывной бомбардировке молекулами. В результате элементу стенки ΔS сообщается за время Δt = 1 с некоторый импульс Ft, который численно равен силе, действующей на ΔS. Отношение этой силы к величине ΔS дает давление, оказываемое газом на стенки сосуда. Вследствие хаотичности движения молекул давление газа на различные участки стенок сосуда одинаково.

Рассмотрим этот процесс детально. Пусть молекула массы m0 движется со скоростью перпендикулярно стенке. После абсолютно упругого соударения со стенкой, молекула будет двигаться в υ обратном направлении с той же скоростью. При этом молекула передает стенке импульс, равный изменению собственного импульса: Δ p

. (5.11) 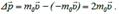За время Δt число молекул, достигших площадки ΔS, равно: 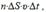где n – концентрация молекул (число молекул в единице объема).

Реально к площадке ΔS молекулы подлетают под разными углами. Однако с учетом полной хаотичности движения можно считать, что в любой момент времени вдоль каждой из 3х осей декартовых координат движется 1/3 молекул, причем половина этих молекул (1/6 от общего числа) движется вдоль данной оси в одну сторону, а другая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔS равно:

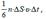а переданный ими импульс:

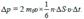(5.12) Тогда давление газа на стенку сосуда

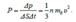. = =(5.13)

Желая подчеркнуть, что под величиной υ понимается средняя скорость движения молекул (хотя молекулы газа обладают безграничным набором скоростей), введем для нее обозначение <υ> и перепишем (5.13) в виде:

. (5.14) 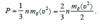Учитывая, что величина 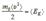представляет собой среднюю кинетическую энергию поступательного хаотического движения молекул, получим:

. (5.15) 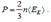Давление в газе, таким образом, определяется средней энергией поступательного хаотического движения молекул.

Уравнения (5.10), (5.14), и (5.15) называются основными уравнениями молекулярно-кинетической теории Сопоставим между собой выражения (5.10) и (5.15). Поскольку левые части (5.10) и (5.15) определяют исходя из разных предпосылок одно и то же давление газа, можно приравнять правые части этих выражений:

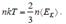Отсюда получим, что

, (5.16)

т.е. температура является мерой средней кинетической энергии хаотического движения молекул идеального газа. Из (5.16) следует, что при Т = 0 и = 0, т.е. при абсолютном нуле, прекращается поступательное движение молекул газа, следовательно, его давление равно нулю. Соотношение (5.16) ñраскрывает молекулярно-кинетический смысл понятия температуры. K Eá

Сделаем в заключение одно замечание. Поступательное движение в пространстве молекулы идеального газа (по определению атомы идеального газа являются материальными точками) описывается тремя независимыми координатами: X, Y и Z. Поэтому говорят, что такая молекула имеет три степени свободы. Вследствие полной хаотичности движения можно, учитывая (5.16), считать, что энергия, приходящаяся на одну степень свободы,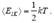

Закон Дальтона: Рассмотрим смесь идеальных газов, заключенных в объеме V при температуре Т. Обозначим массы и молекулярные веса их:

m_1, m_2, m₃ ....m_n

m_1, m_2, m₃.... m_n

Парциальным давлением газа, входящего в газовую смесь, называется то давление, которое имел бы этот газ, если бы он один занимал весь объем сосуда при данной температуре.

Тогда суммарное давление газовой смеси равно сумме парциальных давлений входящих в нее газов - ЗАКОН ДАЛЬТОНА.