Масса
Из-за разницы в числе нейтронов 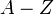 изотопы элемента имеют разную массу
изотопы элемента имеют разную массу 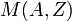 , которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида 12C[сн 2]. Следует отметить, что стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть еще и энергию связи электронов с ядром).
, которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида 12C[сн 2]. Следует отметить, что стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть еще и энергию связи электронов с ядром).
Кроме того, в ядерной физике часто используется энергетический эквивалент массы. Согласно соотношению Эйнштейна, каждому значению массы 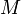 соответствует полная энергия:
соответствует полная энергия:
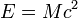 , где
, где  — скорость света в вакууме.
— скорость света в вакууме.
Соотношение между а. е. м. и её энергетическим эквивалентом в джоулях:
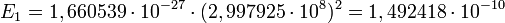 ,
,
а так как 1 электронвольт = 1,602176·10−19 Дж, то энергетический эквивалент а. е. м. в МэВ равен[1][3]:
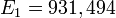 .
.
Изото́пы (от др.-греч. ισος — «равный», «одинаковый», и τόπος — «место») — разновидности атомов (и ядер) какого-либо химического элемента, которые имеют одинаковый атомный номер, но при этом разные массовые числа. Название связано с тем, что все изотопы одного атома помещаются в одно и то же место (в одну клетку) таблицы Менделеева. Химические свойства атома зависят от строения электронной оболочки, которая, в свою очередь, определяется в основном зарядом ядра Z (то есть количеством протонов в нём), и почти не зависят от его массового числа A (то есть суммарного числа протонов Z и нейтронов N). Все изотопы одного элемента имеют одинаковый заряд ядра, отличаясь лишь числом нейтронов. Обычно изотоп обозначается символом химического элемента, к которому он относится, с добавлением верхнего левого индекса, означающего массовое число (например, 12C, 222Rn).
№32 Масса и энергия связи ядра. Удельная энергия связи. Понятие о ядерных силах.
Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С:
1а.е.м = 1.6606 10-27 кг.
А.е.м. выражается через энергетические единицы:
1а.е.м = 1.510-3 эрг = 1.510-10Дж = 931.49 МэВ
Масса ядра всегда меньше суммы масс составляющих его нуклонов.
Энергия связи ядра Eсв(A,Z) это минимальная энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны.
Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)]c2,
где Z - число протонов, (A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z.
Энергия связи ядра, выраженная через массу атома Mат, имеет вид:
Есв(A, Z) = [ZmH + (A - Z)mn - Mат(A, Z)]c2,
где mH - масса атома водорода.
Удельной энергией связи ядра называется энергия связи, приходящаяся на один нуклон Есв/А. На рис. 20 представлен график зависимости удельной энергии связи от массового числа. Анализируя этот график, можно сделать следующие выводы:
1. Удельная энергия связи не является постоянной величиной для различных ядер, т.е. прочность связи нуклонов в различных ядрах различна. Наиболее прочно нуклоны связаны в ядрах с массовыми числами в диапазоне примерно от 40 до 100. Для этой группы ядер удельная энергия связи равна примерно 8,7 МэВ/нуклон.
2. Удельная энергия связи ядер с массовым числом А > 100 уменьшается и для урана составляет 7,6 МэВ.
3. В легких ядрах удельная энергия связи уменьшается с уменьшением числа нуклонов в ядре. Характерным для кривой удельной энергии связи в этой группе ядер является наличие острых максимумов и минимумов. Максимальное значение удельной энергии связи приходится на ядра 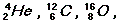 а минимальное – на ядра
а минимальное – на ядра 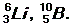
ЯДЕРНЫЕ СИЛЫ - силы взаимодействия между нуклонами; обеспечивают большую величину энергии связи ядер по сравнению с др. системами. Я. с. являются наиб. важным и распространённым примером сильного взаимодействия (СВ). Когда-то эти понятия были синонимами и сам термин "сильное взаимодействие" был введён для подчёркивания огромной величины Я. с. по сравнению с др. известными в природе силами: эл--магн., слабыми, гравитационными. После открытия p-, r- и др. мезонов, гиперо-нов и др. адронов термин "сильное взаимодействие" стали применять в более широком смысле - как взаимодействие адронов. В 1970-х гг. квантовая хромодинамика (КХД) утвердилась как общепризнанная микроскопич. теория СВ. Согласно этой теории, адроны являются составными частицами, состоящими из кварков и глюонов, а под СВ стали понимать взаимодействие этих фундам. частиц.
С др. стороны, Я. с. как силы взаимодействия между нуклонами включают не только СВ, но и эл--магн., слабое и гравитац. взаимодействия нуклонов. С точки зрения совр. теории, эл--магн. и слабое взаимодействия являются проявлениями одного, более фундаментального, электрослабого взаимодействия. Однако при тех пространственно-временных масштабах (~10-13см, ~10-23с), с к-рыми обычно имеют дело в атомных ядрах, единая природа эл--магн. и слабых сил практически не проявляется и их можно рассматривать как независимые. Эти взаимодействия, будучи гораздо слабее СВ, в большинстве ядерных процессов малосущественны, но возможны ситуации, когда их роль становится определяющей. Так, эл--магн. взаимодействие (наиб. существ. часть к-рого - кулоновское отталкивание между протонами), в отличие от СВ, является дальнодействующим. Поэтому обусловленная им положит. кулоновская энергия ядра растёт с увеличением числа частиц А в ядре быстрее, чем отрицат. часть ядерной энергии, обусловленная СВ. В результате тяжёлые ядра становятся при больших А нестабильными - сначала по отношению к делению (см. Деление ядер),а затем и абсолютно нестабильными. Со слабым взаимодействием нуклонов связано такое явление, как несохранение чётности в нуклон-нуклонном рассеянии и в др. ядерных явлениях (см. Несохранение чётности в ядрах). Гравитац. силы, действующие между нуклонами, пренебрежимо малы во всех ядерных явлениях и существенны только в астрофиз. условиях (см. Нейтронные звёзды).
№33 Естественная и искусственная радиоактивность. Виды радиоактивного излучения. Закон радиоактивного распада. Период полураспада.
Естественная радиоактивность — самопроизвольный распад ядер элементов, встречающихся в природе.
Искусственная радиоактивность — самопроизвольный распад ядер элементов, полученных искусственным путем через соответствующие ядерные реакции.
Подвергая радиоактивное излучение действию магнитного поля, Э. Резерфорд выделил два вида лучей: -лучи - тяжелые положительно заряженные (ядра атомов гелия) и β-лучи - легкие отрицательно заряженные частицы (тождественные электронам).
Два года спустя П. Виллард открыл гамма-лучи -нейтральное излучение, где масса покоя равна нулю (аналогично свойствам света, но νγ>>νсв)
Закон радиоактивного распада — физический закон, описывающий зависимость интенсивности радиоактивного распада от времени и количества радиоактивных атомов в образце. Открыт Фредериком Содди и Эрнестом Резерфордом, каждый из которых впоследствии был награжден Нобелевской премией. Они обнаружили его экспериментальным путём и опубликовали в 1903 году в работах «Сравнительное изучение радиоактивности радия и тория»[1] и «Радиоактивное превращение»[2], сформулировав следующим образом[3]: Существует несколько формулировок закона, например, в виде дифференциального уравнения:
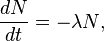
которое означает, что число распадов − dN, произошедшее за короткий интервал времени dt, пропорционально числу атомов N в образце.
Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время T ½, в течение которого система распадается с вероятностью 1/2. Если рассматривается ансамбль независимых частиц, то в течение одного периода полураспада количество выживших частиц уменьшится в среднем в 2 раза. Термин применим только к экспоненциально распадающимся системам.
№34. Ядерные реакции. Деление ядер. Цепная ядерная реакция. Термоядерные реакции, условия их протекания.
Я́дерная реа́кция — процесс образования новых ядер или частиц при столкновениях ядер или частиц. Впервые ядерную реакцию наблюдал Резерфорд в 1919 году, бомбардируя α-частицами ядра атомов азота, она была зафиксирована по появлению вторичных ионизирующих частиц, имеющих пробег в газе больше пробега α-частиц и идентифицированных как протоны. Впоследствии с помощью камеры Вильсона были получены фотографии этого процесса.
По механизму взаимодействия ядерные реакции делятся на два вида:
- реакции с образованием составного ядра, это двухстадийный процесс, протекающий при не очень большой кинетической энергии сталкивающихся частиц (примерно до 10 МэВ).
- прямые ядерные реакции, проходящие за ядерное время, необходимое для того, чтобы частица пересекла ядро. Главным образом такой механизм проявляется при больших энергиях бомбардирующих частиц.
Деле́ние ядра́ — процесс расщепления атомного ядра на два (реже три) ядра с близкими массами, называемых осколками деления. В результате деления могут возникать и другие продукты реакции: лёгкие ядра (в основном альфа-частицы), нейтроны и гамма-кванты. Деление бывает спонтанным (самопроизвольным) и вынужденным (в результате взаимодействия с другими частицами, прежде всего, с нейтронами). Деление тяжёлых ядер — экзотермический процесс, в результате которого высвобождается большое количество энергии в виде кинетической энергии продуктов реакции, а также излучения. Деление ядер служит источником энергии в ядерных реакторах и ядерном оружии.
Цепна́я я́дерная реа́кция — последовательность единичных ядерных реакций, каждая из которых вызывается частицей, появившейся как продукт реакции на предыдущем шаге последовательности. Примером цепной ядерной реакции является цепная реакция деления ядер тяжёлых элементов, при которой основное число актов деления инициируется нейтронами, полученными при делении ядер в предыдущем поколении.
Термоядерная реакция — слияние двух атомных ядер с образованием нового, более тяжелого ядра, за счет кинетической энергии их теплового движения.
Для ядерной реакции синтеза исходные ядра должны обладать относительно большой кинетической энергией, поскольку они испытывают электростатическое отталкивание, так как одноименно положительно заряжены.
Согласно кинетической теории, кинетическую энергию движущихся микрочастиц вещества (атомов, молекул или ионов) можно представить в виде температуры, а, следовательно, нагревая вещество, можно достичь ядерной реакции синтеза.
Подобным образом протекают ядерные реакции естественного нуклеосинтеза в звездах.
Реакции синтеза между ядрами легких элементов вплоть до железа проходят экзоэнергетически, с чем связывают возможность применения их в энергетике, в случае решения проблемы управления термоядерным синтезом.
Прежде всего, среди них следует отметить реакцию между двумя изотопами (дейтерий и тритий) весьма распространенного на Земле водорода, в результате которой образуется гелий и выделяется нейтрон. Реакция может быть записана в виде:
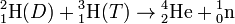 + энергия (17,6 МэВ).
+ энергия (17,6 МэВ).
Выделенная энергия (возникающая из-за того, что гелий-4 имеет очень сильные ядерные связи) переходит в кинетическую энергию, большую часть из которой, 14,1 МэВ, уносит с собой нейтрон как более лёгкая частица[5]. Образовавшееся ядро прочно связано, поэтому реакция так сильно экзоэнергетична. Эта реакция характеризуется наинизшим кулоновским барьером и большим выходом, поэтому она представляет особый интерес для управляемого термоядерного синтеза[1].
Термоядерная реакция также используется в термоядерном оружии.
№35 Статистический метод изучения макросистем, состоящих из многих частиц. Понятие об идеальном газе. Параметры состояния. Уравнение Менделеева – Клапейрона. Изопроцессы в газах.
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют также форму в виде упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц и др.[1].
ПАРАМЕТРЫ СОСТОЯНИЯ (термодинамические параметры) - физ. величины, характеризующие равновесное состояние термодинамич. системы: темп-pa, объём, плотность, давление, намагниченность, электрич. поляризация и др. Различают экстенсивные П. с., пропорциональные объёму (или массе) системы (внутренняя энергия U, энтропия S, энтальпия Н, Гельмголъца энергия, или свободная энергия F, Гиббса энергия G),и интенсивные П. с., не зависящие от массы системы (темп-pa Т, давление Р, концептрация с, хим. потенциал 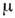 ). В состоянии термодинамич. равновесия П. с. не зависят от времени и пространств. координат. В неравновесном (квазиравновесном) состоянии П. с. могут зависеть от координат и времени.
). В состоянии термодинамич. равновесия П. с. не зависят от времени и пространств. координат. В неравновесном (квазиравновесном) состоянии П. с. могут зависеть от координат и времени.
Термодииамич. состояние определяется заданием совокупности независимых П. с. Однако не все П. с. являются независимыми. Уравнение состояния выражает зависимые П. с. через независимые; напр., давление является ф-цией темп-ры и объёма Р = P(V, Т). Объём является внешним П. с., т. к. определяется положением внеш. тел (стенки сосуда, положение поршня). Темп-pa зависит только от внутр. состояния системы и наз. внутренним П. с. В общем случае Р = Р(а 1, ..., ап, Т), где аi - внеш. П. с.
Элементарная работа 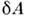 термодинамич. системы определяется П. с., напр. для жидкости или газа
термодинамич. системы определяется П. с., напр. для жидкости или газа 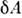 = PdV, а в общем случае
= PdV, а в общем случае 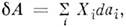 где Хi = Хi(а 1, ..., ап, Т) - обобщённые силы, являющиеся также П. с. Каждому набору независимых П. с. соответствуют определ. потенциалы термодинамические (характеристические функции), определяющие все термодинамич. свойства системы и зависящие лишь от выбранных параметров; напр., внутр. энергия U = U(V, S), энтропия S = S(V, U), энтальпия H = Н(Р, S), энергия Гельмгольца (свободная энергия F = F(V, Т), энергия Гиббса G = G(P, T, N), N - число частиц. Для многокомпонентных систем нужно учитывать ещё дополнит. П. с.: концентрации компонент сi или их хим. потенциалы
где Хi = Хi(а 1, ..., ап, Т) - обобщённые силы, являющиеся также П. с. Каждому набору независимых П. с. соответствуют определ. потенциалы термодинамические (характеристические функции), определяющие все термодинамич. свойства системы и зависящие лишь от выбранных параметров; напр., внутр. энергия U = U(V, S), энтропия S = S(V, U), энтальпия H = Н(Р, S), энергия Гельмгольца (свободная энергия F = F(V, Т), энергия Гиббса G = G(P, T, N), N - число частиц. Для многокомпонентных систем нужно учитывать ещё дополнит. П. с.: концентрации компонент сi или их хим. потенциалы 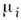 . Для многофазных систем каждая фаза описывается своим парциальным термодинамич. Потенциалом.
. Для многофазных систем каждая фаза описывается своим парциальным термодинамич. Потенциалом.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
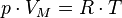 ,
,
где
-
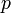 — давление,
— давление, -
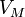 — молярный объём,
— молярный объём, -
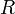 — универсальная газовая постоянная
— универсальная газовая постоянная -
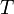 — абсолютная температура,К .
— абсолютная температура,К .
Так как 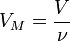 , где
, где 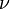 — количество вещества, а
— количество вещества, а 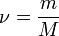 , где
, где 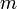 — масса,
— масса, 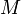 — молярная масса, уравнение состояния можно записать:
— молярная масса, уравнение состояния можно записать:
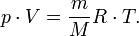
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Уравнение, выведенное Клапейроном содержало некую неуниверсальную газовую постоянную  , значение которой необходимо было измерять для каждого газа:
, значение которой необходимо было измерять для каждого газа:
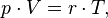
Менделеев же обнаружил, что  прямо пропорциональна
прямо пропорциональна 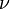 , коэффициент пропорциональности
, коэффициент пропорциональности  он назвал универсальной газовой постоянной.
он назвал универсальной газовой постоянной.
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.
Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении (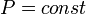 )
)
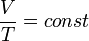
Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме (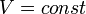 ). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
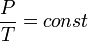
Линия, изображающая изохорный процесс на диаграмме, называется изохорой.
Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.
Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре (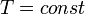 )(
)(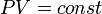 ). Изотермический процесс описывается законом Бойля — Мариотта:
). Изотермический процесс описывается законом Бойля — Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
№36. Вывод основного уравнения МКТ газов. Молекулярно- кинетическое истолкование давления и температуры. Закон Дальтона.
Вывод основного уравнения МКТ
Пусть имеется кубический сосуд с ребром длиной 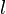 и одна частица массой
и одна частица массой 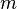 в нём.
в нём.
Обозначим скорость движения 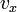 , тогда перед столкновением со стенкой сосуда импульс частицы равен
, тогда перед столкновением со стенкой сосуда импульс частицы равен 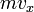 , а после —
, а после — 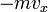 , поэтому стенке передается импульс
, поэтому стенке передается импульс 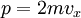 . Время, через которое частица сталкивается с одной и той же стенкой, равно
. Время, через которое частица сталкивается с одной и той же стенкой, равно 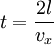 .
.
Отсюда следует:
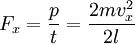
Так как давление 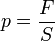 , следовательно сила
, следовательно сила 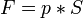
Подставив, получим: 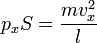
Преобразовав: 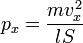
Так как рассматривается кубический сосуд, то 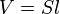
Отсюда:
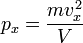 .
.
Соответственно, 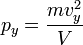 и
и 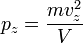 .
.
Таким образом, для большого числа частиц верно следующее: 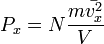 , аналогично для осей y и z.
, аналогично для осей y и z.
Поскольку 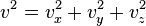 , то
, то 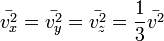 . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.
. Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.
Отсюда 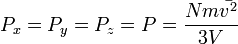
или 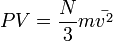 .
.
Пусть 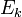 — среднее значение кинетической энергии всех молекул, тогда:
— среднее значение кинетической энергии всех молекул, тогда:
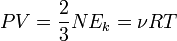 , откуда, используя то, что
, откуда, используя то, что 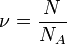 (количество вещества), а
(количество вещества), а 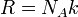 , имеем
, имеем 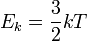 .
.
 2015-05-18
2015-05-18 7818
7818