2015-05-18
1449
По экспериментальным данным исследовать зависимость показателя y от факторов x1, x2:
1) Составить матрицы межфакторной корреляции К и кросскорреляции М;
2) Найти линейное уравнение регрессии в стандартизированном и натуральном виде и среднюю эластичность по обоим факторам;
3) Оценить качество модели по критерию Фишера, а также необходимость включения в регрессионную модель одного фактора после включения другого по частному критерию Фишера (α =0,05).
Зависимость чистого дохода (y) от оборота капитала (x1) и от численности служащих (x2) по 16 компаниям. Заданы эмпирические средние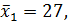 
, 
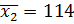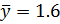, среднеквадратические отклонения 
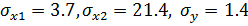, и коэффициенты парных корреляций 
.
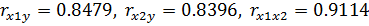Решение.
Составим матрицы межфакторной корреляции К
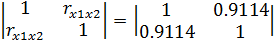
и кросскорреляции М:
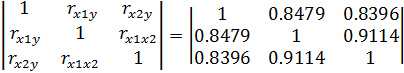
Линейное уравнение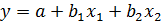 
Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:
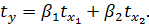
Для этого рассчитаем β-коэффициент:
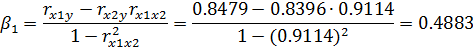
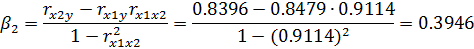
Получим уравнение в стандартизированном виде:
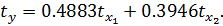
Используя формулы перехода от β к b рассчитаем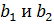 
:
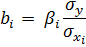
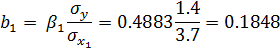
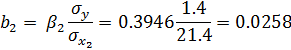
Получим значение
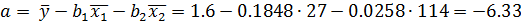
Теперь мы можем записать уравнение в натуральном виде:
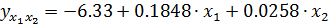
Найдем среднюю эластичность:
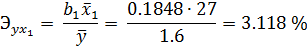
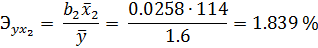
С увеличением на 1% оборота капитала зависимость чистого дохода увеличивается на 3.12%, а с увеличением на 1% численности служащих он увеличивается на 1.84%. Очевидно, что оборот капитала (х1) оказывает больший эффект на чистый доход, чем численность служащих (х2).
Рассчитаем линейный коэффициент множественной корреляции выполним с использованием коэффициентов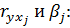 
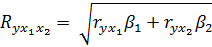
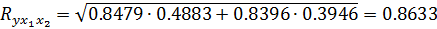
Теперь проверим частные критерии Фишера.
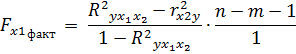
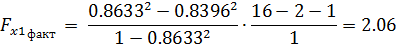
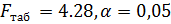
Сравнивая табличное значение и фактическое критерия Фишера приходим к выводу о нецелесообразности включения в модель фактора x1 (оборота капитала) после фактора х2, так как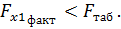 
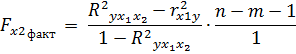
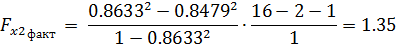
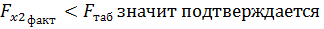Н0 о целесообразности включения в модель фактора x2.
Это значит мы можем исключить такой фактор как оборот капитала (х1). Парная регрессионная модель зависимости чистого дохода (у) и численности служащих (х2) является достаточно статистически значимой.
