Задача 1. По 30 территориям России имеются данные, представленные в табл

По 30 территориям России имеются данные, представленные в табл. 2.1.

Признак	Среднее значение	Среднее квадратическое отклонение	Линейный коэффициент парной корреляции
Среднедневной душевой доход, руб., у	86,8	11,44	-
Среднедневная заработная плата одного работающего, руб., х₁	54,9	5,86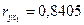
Средний возраст безработного, лет, х₂	33,5	0,58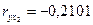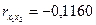

Требуется:

1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с β₁ и β₂, пояснить различия между ними.

2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.

3.Рассчитать общий и частные F-критерии Фишера.

Решение:

1. Линейное уравнение множественной регрессии у от х₁ и х₂ имеет вид: у = а+b₁∙х₁+b_2∙x₂. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: 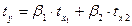. Расчет β-коэффициентов выполним по формулам:

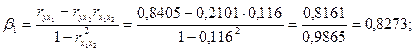
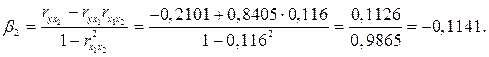
Получим уравнение: t_y=0,8273 t_x₁ -0,1141 t_x2.

Для построения уравнения в естественной форме рассчитаем b₁ и b_2, используя формулы для перехода от β_i к b_i:

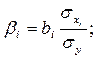
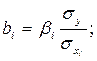
Значение а определим из соотношения:

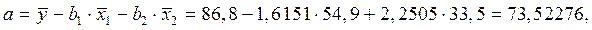
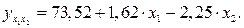
Для характеристики относительной силы влияния х₁ и х₂ на у рассчитаем средние коэффициенты эластичности:

;

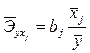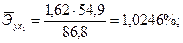
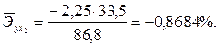
С увеличением средней заработной платы на 1 % от ее среднего уровня средний душевой доход у возрастает на 1,02 % от своего среднего уровня; при повышении среднего возраста безработного х₂ на 1 % среднедушевой доходу снижается на 0,87 % от своего среднего уровня. Очевидно, что сила влияния средней заработной платы х₁ на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х₂ К аналогичным выводам о силе связи приходим при сравнении модулей значений β₁и β₂:

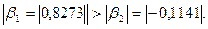Различия в силе влияния фактора на результат, полученные при сравнени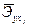и . и 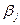, объясняются тем, что коэффициент эластичности исходит из соотношения средних: 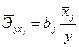, а β-коэффициент - из соотношения средне- квадратических отклонений .

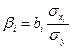2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:

;

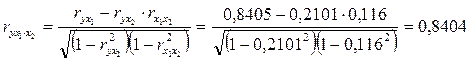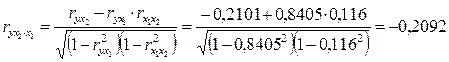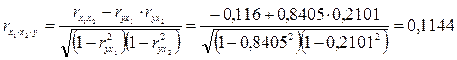Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (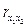 = -0,116) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:

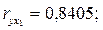
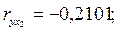
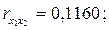
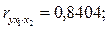
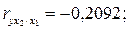
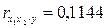Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 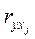и β_j:

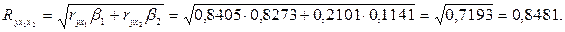Зависимость у от x₁ и x₂ характеризуется как тесная, в которой 72 % вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28 % от общей вариации у.

3. Общий F-критерий проверяет гипотезу H₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R² = 0):

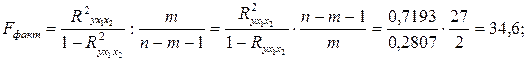
F_табл=3,4; α=0,05.

Сравнивая F_табл и F_факт приходим к выводу о необходимости отклонить гипотезу H₀, так как F_табл=3,4<F_факт⁼34,6. С вероятностью 1 - α= 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 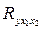, которые сформировались под неслучайным воздействием факторов х₁ и F х₂. Частные F-критери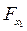и - и 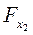оценивают статистическую значимость присутствия факторов х₁ и х₂ в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. 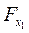оценивает целесообразность включения в уравнение фактора х₁ после того, как в него был включен фактор х₂. Соответственно 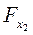указывает на целесообразность включения в модель фактора x₂ после фактора х₁:

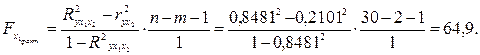
Сравнивая F_табли F_факт, приходим к выводу о целесообразности включения в модель фактора х₁ после фактора х₂, так как 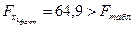. Гипотезу 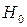о несущественности прироста 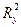за счет включения дополнительного фактора х₁ отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х₁ после фактора х₂.

Целесообразность включения в модель фактора х₂ после фактора х₁ проверяет :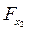

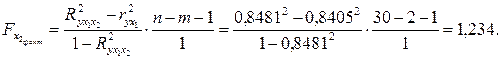
Низкое значение 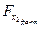(немногим больше 1) свидетельствует о статистической незначимости прироста 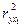за счет включения в модель фактора х₂ после фактора х₁. Следовательно, подтверждается нулевая гипотеза 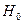о нецелесообразности включения в модель фактора х₂ (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор х₂ (средний возраст безработного).