Для задачи 3 выполнить дисперсионный анализ
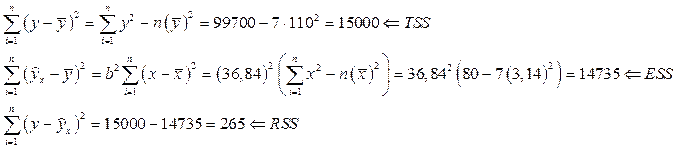 Заполним таблицу дисперсного анализа
Заполним таблицу дисперсного анализа
| Источники вариации | Число степеней свободы | Сумма квадратов отклонений | Дисперсия на 1 степень свободы | F отн | |
| Факт. | Табл. α=0,05 | ||||
| Общая TSS | 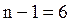
| – | – | – | |
| Объясн. ESS | 1 (к1) | 6,61 | |||
| Остаточн. RSS | 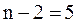 (к2) (к2)
|
Критерий Фишера равен:
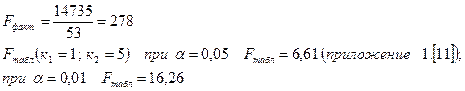
Fфакт> Fтабл. как при 5%, так и при 1% уровне значимости уравнения регрессии. 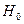 – нулевая гипотеза (b = 0; rxy = 0)отвергается. Между х и у существует линейная зависимость.
– нулевая гипотеза (b = 0; rxy = 0)отвергается. Между х и у существует линейная зависимость.
Если Fфакт< Fтабл., то вероятность нулевой гипотезы выше заданного уровня, и она не может быть отклонена без серьезного риска, сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется, а отклоняется проверяемая гипотеза Н1.
Величина F-критерия связана с коэффициентом детерминации R2.
Объясненную сумму квадратов (ESS) можно вычислить как 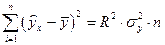 , а остаточную сумму (RSS) -
, а остаточную сумму (RSS) - 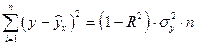
Тогда значение критерия Фишера
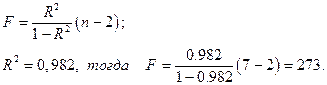
 2015-05-18
2015-05-18 428
428








