Общие для обоих пунктов соображения:
0) Допустим, страна хочет произвести 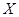 единиц Икса. Вторая координата на КПВ в точке
единиц Икса. Вторая координата на КПВ в точке 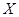 показывает максимально возможное производство Игрека при условии, что производится
показывает максимально возможное производство Игрека при условии, что производится 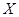 единиц Икса. Таким образом, чтобы найти КПВ, нам нужно решить следующую задачу: при каждом значении
единиц Икса. Таким образом, чтобы найти КПВ, нам нужно решить следующую задачу: при каждом значении 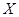 понять, сколько и каких заводов нужно построить стране, и как распределить между ними производство Игрека, так чтобы суммарное производство Игрека было максимальным.
понять, сколько и каких заводов нужно построить стране, и как распределить между ними производство Игрека, так чтобы суммарное производство Игрека было максимальным.
1) Заметим, что при любом 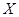 страна не будет строить больше одного завода по производству Игрека. Предположим противное – построено несколько заводов и на них в сумме произведен некий объем
страна не будет строить больше одного завода по производству Игрека. Предположим противное – построено несколько заводов и на них в сумме произведен некий объем 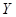 Игрека. Обозначим за
Игрека. Обозначим за 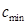 минимальные удельные затраты труда на один Игрек среди построенных заводов. Тогда если бы страна построила всего один завод с удельными затратами
минимальные удельные затраты труда на один Игрек среди построенных заводов. Тогда если бы страна построила всего один завод с удельными затратами 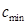 , и произвела на нем объем
, и произвела на нем объем 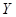 Игрека, то затраты труда как на производство Игрека, так и на строительство заводов были бы меньше. Высвободившийся труд можно направить на производство дополнительных единиц Игрека, а значит, изначальное решение не было оптимальным. Противоречие.
Игрека, то затраты труда как на производство Игрека, так и на строительство заводов были бы меньше. Высвободившийся труд можно направить на производство дополнительных единиц Игрека, а значит, изначальное решение не было оптимальным. Противоречие.
2) Таким образом, задача сводится к тому, чтобы при каждом 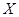 понять, (единственный) завод какого типа нужно строить стране, чтобы максимизировать производство Игрека.
понять, (единственный) завод какого типа нужно строить стране, чтобы максимизировать производство Игрека.
а) Зафиксируем 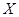 . После производства Икса у страны остается в распоряжении
. После производства Икса у страны остается в распоряжении 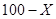 единиц труда. Если построить завод с первой технологией, то страна сможет произвести
единиц труда. Если построить завод с первой технологией, то страна сможет произвести 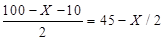 единиц Игрека. Если построить завод со второй технологией, то страна сможет произвести
единиц Игрека. Если построить завод со второй технологией, то страна сможет произвести 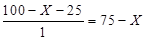 единиц Игрека. Если построить завод с третьей технологией, то страна сможет произвести
единиц Игрека. Если построить завод с третьей технологией, то страна сможет произвести 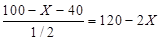 единиц Игрека.
единиц Игрека.
То, какой завод строить, определяется просто тем, какое из чисел 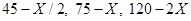 больше при данном
больше при данном 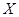 .
.
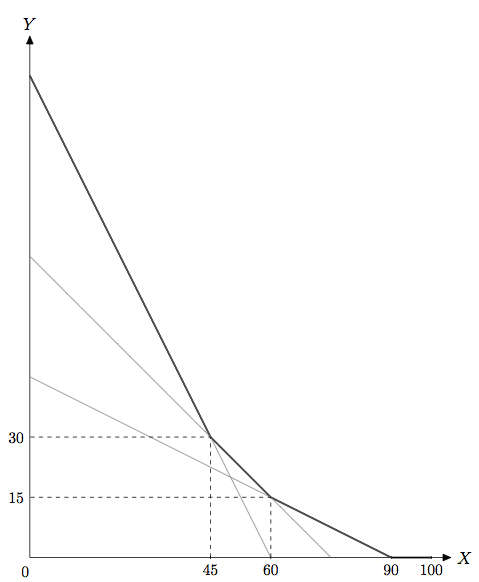 Проще всего это сделать, построив графики этих трех прямых. Искомой КПВ будет ломаная линия, являющаяся «верхней огибающей» трех этих графиков. Проведя такой анализ, видим, что при
Проще всего это сделать, построив графики этих трех прямых. Искомой КПВ будет ломаная линия, являющаяся «верхней огибающей» трех этих графиков. Проведя такой анализ, видим, что при 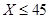 надо строить завод с третьей технологией, при
надо строить завод с третьей технологией, при 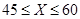 - завод со второй технологией, а при
- завод со второй технологией, а при 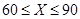 - завод с первой технологией. При
- завод с первой технологией. При 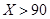 у страны нет достаточного количества ресурсов для постройки заводов), и максимальное производство Игрека будет равняться нулю.
у страны нет достаточного количества ресурсов для постройки заводов), и максимальное производство Игрека будет равняться нулю.
Таким образом, уравнение КПВ имеет вид

Ее график – это ломаная с точками излома (45, 30), (60,15), (90,0).
б) Если страна тратит 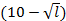 единиц труда на постройку завода, то для производства Y единиц продукции Игрек потребуется lY рабочей силы. Значит, общая рабочая сила раскладывается на слагаемые, задействованные в разных видах деятельности, следующим образом:
единиц труда на постройку завода, то для производства Y единиц продукции Игрек потребуется lY рабочей силы. Значит, общая рабочая сила раскладывается на слагаемые, задействованные в разных видах деятельности, следующим образом:
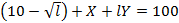 . Отсюда
. Отсюда 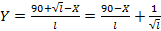 .
.
1) Заметим, что при 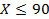 эта функция убывает по l, то есть если мы хотим произвести меньше 90 единиц Х, то нужно выбирать минимально возможный
эта функция убывает по l, то есть если мы хотим произвести меньше 90 единиц Х, то нужно выбирать минимально возможный 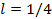 . КПВ тогда будет иметь уравнение
. КПВ тогда будет иметь уравнение 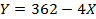 .
.
2) Функцию Y можно записать как 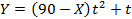 , где
, где 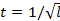 . Если
. Если 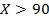 , то это парабола с ветвями вниз относительно t, вершина которой достигается при
, то это парабола с ветвями вниз относительно t, вершина которой достигается при 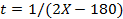 . Согласно условию задачи, t должно попасть в отрезок [1/2; 2], что эквивалентно попаданию X в отрезок [90,25; 91]. Получаем, что на данном участке уравнение КПВ имеет вид
. Согласно условию задачи, t должно попасть в отрезок [1/2; 2], что эквивалентно попаданию X в отрезок [90,25; 91]. Получаем, что на данном участке уравнение КПВ имеет вид 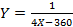 .
.
3) Что происходит при 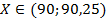 ? Парабола, описанная выше, достигает своей вершины вне этих множеств, значит, нужно выбрать ближайшую к вершине точку, то есть
? Парабола, описанная выше, достигает своей вершины вне этих множеств, значит, нужно выбрать ближайшую к вершине точку, то есть 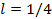 . При этом соответствующий участок КПВ будет описываться уравнением
. При этом соответствующий участок КПВ будет описываться уравнением 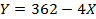 .
.
4) Что если 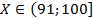 ? Во-первых, заметим, что если страна произведет
? Во-первых, заметим, что если страна произведет 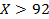 , то не сможет построить ни одного завода, так как
, то не сможет построить ни одного завода, так как 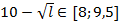 — на строительство завода нужно не меньше 8 единиц труда. Значит, для производства ненулевого Y нужно произвести не больше 92 единиц X. Осталось рассмотреть
— на строительство завода нужно не меньше 8 единиц труда. Значит, для производства ненулевого Y нужно произвести не больше 92 единиц X. Осталось рассмотреть 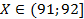 . При таких значениях X парабола, описанная выше, достигает своей вершины вне допустимого множества, значит, нужно выбрать ближайшую к вершине точку, то есть
. При таких значениях X парабола, описанная выше, достигает своей вершины вне допустимого множества, значит, нужно выбрать ближайшую к вершине точку, то есть 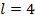 . При этом соответствующий участок КПВ будет описываться уравнением
. При этом соответствующий участок КПВ будет описываться уравнением 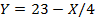 .
.
В итоге имеем уравнение КПВ:
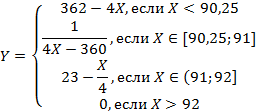
График выглядит следующим образом:
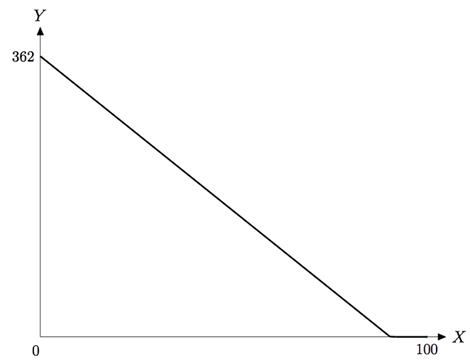
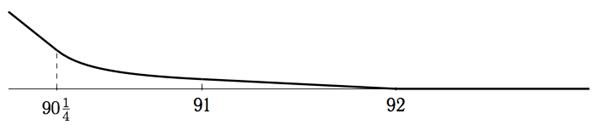
В месте вхождения КПВ в ось X линия выглядит так крупным планом:
 2015-05-18
2015-05-18 531
531








