Средняя – это статистический показатель «середины» или «центра» исследуемых данных. Это важнейший статистический показатель, используемый для обобщения данных. Среднее значение дает представление о «центральном» значении в интервале изменения изучаемого показателя.
В экономическом анализе используются средние:
- средняя арифметическая простая;
- средняя арифметическая взвешенная;
- средняя гармоническая;
- средняя квадратическая.
Средняя арифметическая простая равна простой сумме отдельных значений осредняемого показателя, деленной на общее число этих значений:
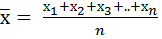 (4)
(4)
Пример. Найти среднюю выработку одного рабочего, если численность рабочих составила 15 человек и индивидуальная выработка каждого рабочего составила: 21,20,20,19,21,19,18,22,19,20,21,20,18,19,20 (шт).
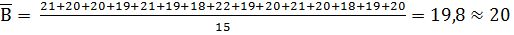 шт.
шт.
Средняя арифметическая взвешенная – это средняя сгруппированных величин:
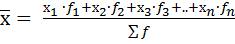 =
= 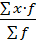 , (5)
, (5)
где 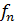 - удельные веса признаков;
- удельные веса признаков;
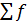 – общая численность единиц совокупности.
– общая численность единиц совокупности.
Пример. В таблице 5 представлена выработка рабочих и распределение численности рабочих по выработке. Определить среднюю выработку на основе применения средней арифметической взвешенной.
Таблица 5 – Распределение рабочих по выработке
| Выработка за смену одним рабочим (x), шт | Число рабочих (веса) (f) | 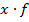
|
| Итого | ||
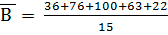 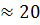 шт. шт.
|
Средняя гармоническая – это средневзвешенная из варьирующих обратных значений признака.
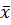 =
= 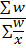 (6)
(6)
Пример.
Таблица 6 - Определить среднюю цену яблок по трем магазинам.
| магазин | Исходные данные | Расчетные значения | |
| Ц за 1 кг яблок, руб. (x) | Выручка, руб. (f) | 
| |
| 3060: 17 = 180 | |||
| 2800: 20 = 140 | |||
| 1920: 24 = 80 | |||
| Итого | |||
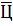 = 7780: 400 = 19,45 руб = 7780: 400 = 19,45 руб
|
Средняя геометрическая применяется для определения средних темпов изменения в рядах динамики и в рядах распределения на основе относительных цепных темпов роста.
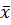 =
= 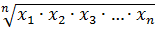 (7)
(7)
 2015-05-18
2015-05-18 360
360








