2015-05-18
484
Сущность способа состоит в том, что для определения величин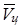 
и 
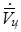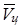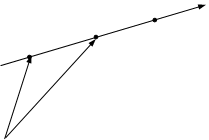
используют изменения векторов, определяющих положение цели, накопленные за некоторый отрезок времени. Особенность этого способа состоит в том, что расчетные формулы для определения и 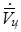зависят от принятой гипотезы о движении цели. Рассмотрим, как определяется `Vц применительно к первой гипотезе о движении цели (`Vц = const), используя для этого рис.4, на котором показаны положения цели на траектории её движения в различные моменты времени и положение ЛА (точка В).
Применим формулу разложения вектор-функции `Dц в ряд Маклорена для моментов времени t = ‑t 1и t = ‑ t 2можнозаписать:
t= 0 `Vц
t= -t 2
t= -t 1
`Dц (- t 2)
`Dц (- t 1)
B
Рис.4
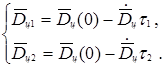
(1)
Из (1) получаем:
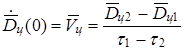. (2)
Используя рис.2, для моментов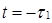 
и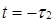 
определяем:
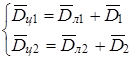. (3)
Из формул (2) и(3) получаем:
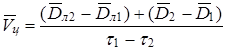(4)
Разность (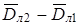
) - это перемещение ЛА за время 
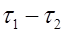. Ее можно определить с помощью системы счисления пути. Дальности `D 1 и `D 2 определяются с помощью визирных устройств.
Рассмотрим теперь определение 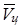и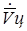 
применительно ко второй гипотезе о движении цели (
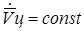), используя рис.5.
 |
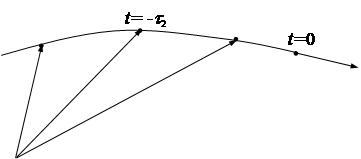t= -t 1 t= -t 3
`Dц (- t 2)
`Dц (- t 1) `Dц (- t 3) `Vц
В
Рис.5
Применяя формулу разложения вектор-функции `Dц (t) в ряд Маклорена для моментов времени 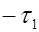t=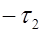 
, t= 
, t=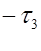 
, получим:
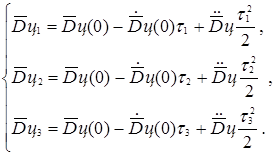(5)
Считая, что в системе (5) три неизвестные величины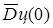 
, 
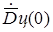и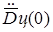 
, можно определить из неё интересующие нас две последние:
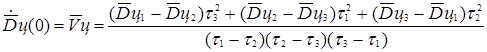, (6)
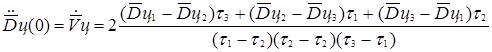.(7)
Используя выражения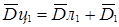 
, 
, 
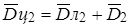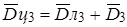(см. формулы 3) для подстановки их в (6) и (7), можно выразить величины 
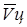и 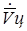через дальности до цели и перемещения ЛА за соответствующие промежутки времени по аналогии с формулой (4).
