Примеры р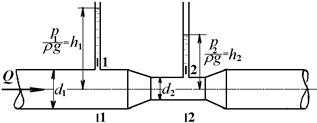ешения задач. Пример № 7.1. Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис

Пример № 7.1.

Определить расход жидкости Q в горизонтальном трубопроводе диаметром d₁ = 0,2 м, имеющем сужение диаметром d₂ = 0,12 м (рис. 7.1). Разность показаний пьезометров D h = 250 мм.

Дано: d₁ = 0,02 м;

d₂ = 0,12 м;

D h = 250 мм = 0,25 м.

Рисунок 7.1 Определить: Q.

Решение

Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 1-1 и 2-2:

z₁ + 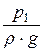+ a₁ × 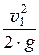= z₂ + 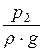+ a₂ × .

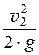Для горизонтального трубопровода z₁ = z₂. Обозначим пьезометрические высоты h₁ = 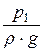, а h₂ = 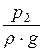. Разность показаний пьезометров равна D h = h₁ - h₂. Уравнение Бернулли принимает вид:

D h = a₂ × 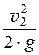- a₁ × .

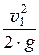Из уравнения неразрывности v ₁ × w₁ = v ₂ × w₂ выразим скорость во втором сечении:

v ₂ = v ₁ × .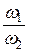

Для круглого напорного трубопровода площадь живого сечения потока w = 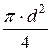. Тогда

v ₂ = v ₁ × .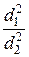

Подставляя это выражение в уравнение Бернулли имеем:

D h = a₂ × 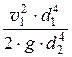- a₁ × .

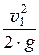Считаем, что течение жидкости в трубопроводе турбулентное. Принимаем коэффициент Кориолиса a₁ = a₂ = a = 1,1.

D h = a × .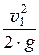

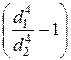v ₁ = 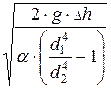= = 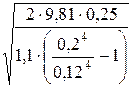0,815 (м/с).

Объёмный расход равен:

Q = v ₁ × w₁ = v ₁ × 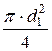= 0,815 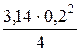= 0,0256 (м³/с).

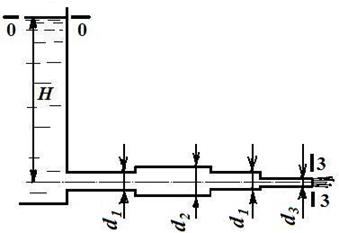
Пример № 7.2. Жидкость вытекает из резервуара большого сечения по горизонтальному трубопроводу переменного сечения. Определить расход Q в горизонтальном трубопроводе (рис. 7.2), скорость на каждом из участков v_i и построить пьезометрическую линию 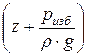. Напор над центром отверстия, к которому присоединён трубопровод, Н равен 5 м. Диаметры различных участков трубопровода соответственно равны: d₁ = 15 мм, d₂ = 20 мм, d₃ = 10 мм.

Дано: Н = 5 м;

d₁ = 15 мм = 0,015 м;

d₂ = 20 мм = 0,020 м;

d₃ = 10 мм = 0,010 м.

Определить: Q, v₁, v₂, и v₃.

Рисунок 7.2 Решение

Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 0-0 (свободная поверхность жидкость в резервуаре, из которого истекает жидкость) и 3-3 (выходное сечение трубопровода):

z₀ + 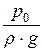+ a₀ × 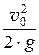= z₃ + 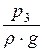+ a₃ × .

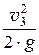Здесь р₀ – давление на свободную поверхность жидкости в открытом резервуаре равно атмосферному давлению, то есть р₀ = р_бар. р₃ – давление в выходном сечении трубопровода. Оно равно давлению той среды, куда происходит истечение. В данном случае р₃ = р_бар.

Горизонтальную плоскость сравнения совместим с осью трубопровода переменного сечения. Тогда z₀ = Н, а z₃ = 0.

Скорость на свободной поверхности жидкости в резервуаре v₀ пренебрежимо мала по сравнению со скоростью жидкости в трубопроводе переменного сечения v_i. Поэтому полагаем, что v₀» 0.

Принимаем, что коэффициент Кориолиса a. ₃ =1,0. (На практике мы обычно имеем дело с турбулентным движением жидкости.). Уравнение Бернулли имеет вид:

Н + 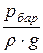+ 0 = 0 + 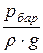+ 1 ×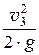

или

Н = .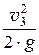

Отсюда

v₃ = 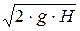= = 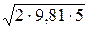9,9 (м/с).

Используя уравнение неразрывности течения определяем расход жидкости в трубопроводе:

Q = v₃ × w₃ = v × 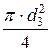= 9,9 × 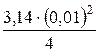= 0,00078 (м³/с).

Используя это же уравнение, определяем скорости на участках диаметром d₁ и d₂:

Q = v₁ × w₁. Þ v₁ = 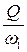= = 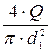= 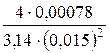4,42 (м/с);

Q = v₂ × w₂. Þ v₂ = 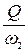= = 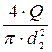= 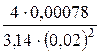2,48 (м/с).

Пьезометрическую линию строят, исходя из следующих положений. Поскольку задача решается без учёта потерь энергии, то напорная линия (линия полной энергии) - 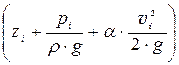будет представлять собой горизонтальную прямую, являющуюся продолжением свободной поверхности воды в сечении 0-0. Пьезометрическая линия 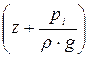расположиться ниже напорной линии на величину 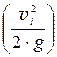в каждом сечении. Таким образом, отложив вниз от напорной линии величины 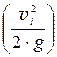в сечениях, соответствующих изменению диаметра трубопровода, получим ряд точек, соединив которые построим пьезометрическую линию. При этом

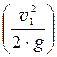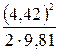= = 0,987 (м);

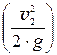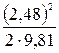= = 0,312 (м);

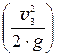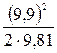= = 5 (м).

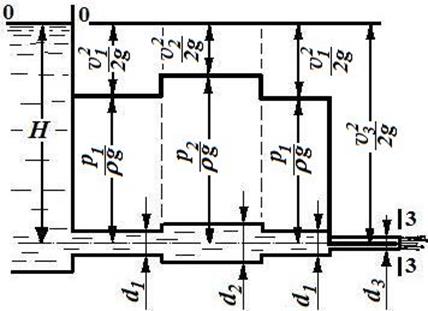
Рисунок 7.3 – Построение пьезометрической линии