Основные теоретические сведения. Уравнение Бернулли представляет собой закон сохранения механической энергии для потока идеальной жидкости

Уравнение Бернулли представляет собой закон сохранения механической энергии для потока идеальной жидкости. Каждый член этого уравнения представляет собой удельную энергию.

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:

r × g × z₁ + р₁ + r × a₁ × 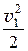= r × g × z₂ + р₂ + r × a₂ × 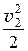= const, (7.1)

где r × g × z – гравитационное давление;

р – статическое давление;

r × 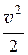– динамическое давление;

a - коэффициент кинетической энергии (коэффициент Кориолиса).

В этой форме представления каждый член уравнения имеет размерность давления (Па) и представляет собой энергию, отнесённую к единице объёма.

Величина коэффициента Кориолиса отражает степень неравномерности распределения скоростей по сечению потока.

При прямолинейном турбулентном движении в трубах a = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса a равным 1,1 или 1. При прямолинейном ламинарном движении в трубах a = 2.

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:

z + 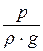+ a × 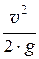= Н = const, (7.2, а)

или для двух произвольных сечений

z₁ + 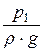+ a₁ × 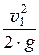= z₂ + 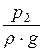+ a₂ × 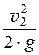= Н = const. (7.2, б)

где z – удельная потенциальная энергия положения;

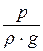– удельная потенциальная энергия давления;

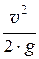– удельная кинетическая энергия;

Н – полная удельная энергия потока.

Каждое слагаемое в уравнении Бернулли в форме напоров имеет размерность длины (м) и представляет собой энергию, отнесённую к единицевеса (1 Н), то есть удельнуюэнергию. Единица измерения этой величины = = .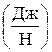

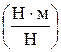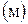С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Так как все члены уравнения Бернулли в форме напоров имеют линейную размерность и их можно интерпретировать как высоты:

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

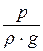– высота давления, если в уравнении Бернулли р – это полное (или абсолютное) давление. Если в уравнении р – избыточное давление, то величина 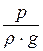называется пьезометрической высотой;

a × 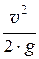– скоростная (или динамическая) высота.

Н – полная высота в данном сечении потока.

Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения (геометрической), давления ( или пьезометрической) и скоростной – есть величина постоянная.

На практике часто используют понятие напора: 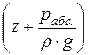- гидростатический напор, 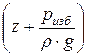- пьезометрический напор, 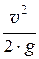- динамический напор, 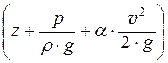- гидродинамический напор.