2015-05-18
4461
Пример 1. Алгебра N = (N; +) не является группой, так как не выполняются аксиомы G2 и G3.
Пример 2. Алгебра N = (N; ×) не является группой, так как нарушается аксиома G3.
Пример 3. Доказать, что алгебры Z = (Z; +), Q = (Q; +), R = (R; +), C = (C; +) являются аддитивными бесконечными абелевыми группами.
Доказательство. Покажем, например, что Z = (Z; +) является аддитивной бесконечной абелевой группой. В самом деле, выполняются аксиомы:
G1. (" z 1, z 2, z 3ÎZ)[(z 1 + z 2) + z 3 = z 1+ (z 2 + z 3)].
G2. ($0ÎZ)(" z ÎZ)[0 + z = z + 0 = z ].
G3. (" z ÎZ)($(-z)ÎZ)[(-z) + z = z + (-z) = 0].
G4. (" z 1, z 2ÎZ)[ z 1+ z 2 = z 2+ z 1].
Кроме того, множество Z - бесконечное.
Что требовалось доказать.
Пример 4. Доказать, что алгебры Q* = (Q*; ×), R* = (R*; ×), C* =(C*; ×) являются мультипликативными абелевыми бесконечными группами.
Доказательство. Докажем, например, что алгебра C* =(С*; ×), где С* = C\{0} является мультипликативной абелевой бесконечной группой. Для этого проверяем выполнение аксиом G1 - G4. Имеем:
G1. (" c 1, c 2, c 3ÎC*)[(c 1× c 2)× c 3 = c 1×(c 2× c 3)].
G2. ($1ÎC*)(" c ÎC*)[1× c = c ×1 = c ].
|
|
|
G3. (" c ÎC*)($ c -1ÎC*)[ c -1× c = c× c -1 =1].
G4. (" c 1, c 2ÎC*)[ c 1× c 2 = c 2× c 1].
Кроме того, С* - бесконечное множество.
Что требовалось доказать.
Заметим, что алгебры Q = (Q; ×), R = (R; ×), C = (C; ×) не являются группами, так как нарушается аксиома G3 (для 0 не существует обратного элемента, поскольку элемент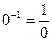 
не определяется в этих множествах).
Пример 5. Алгебра Z = (Z; ×) не является группой, так как аксиома G3 не выполняется.
Пример 6. Из свойств операций над подстановками Ф n следует, что алгебра ({Ф n }; ×) является мультипликативной группой конечного порядка n!. Эта группа называется симметрической и обозначается через S n.
Примеры 7 - 12. Теория геометрических преобразований плоскости (см. курс геометрии) нам представляет следующие бесконечные мультипликативные группы: 7) D = (D; ×)-группа всех движений плоскости; 8) T = (Т; ×) - группа всех параллельных переносов плоскости; 9) Roa = (R oa; ×)-группа всех вращений плоскости вокруг точки О; 10) A = (A; ×)-группа аффинных преобразований плоскости; 11) Ð = (Р; ×)-группа проективных преобразований плоскости; 12) F = (F; ×)-группа симметрий геометрической фигуры.
Пример 13. Обозначим через R[ x ] - множество всех многочленов от одной переменной х с коэффициентами из множества действительных чисел R. Тогда покажем, что алгебра R[ x ] = (R[ x ]; +) является аддитивной бесконечной абелевой группой. В самом деле, выполняются аксиомы:
G1. (" p (x), q (x), r (x)ÎR[ x ])[{ p (x) + q (x)}+ r (x) = p (x) + { q (x) + r (x)}].
G2. ($0(x) = 0ÎR[ x ])(" p (x)ÎR[ x ])[0(x) + p (x) =p (x) + 0(x) =p (x)].
G3. (" p (x)ÎR[ x ])(${- p (x)}ÎR[ x ])[{ -p (x)} + p (x) = p (x)+{ -p (x)}=0(x)].
G4. (" p (x), q (x)ÎR[ x ])[ p (x) + q (x) =q (x) + p (x)].
|
|
|
Кроме того, множество R[ x ] - бесконечное.
Что требовалось доказать.
Пример 14. Тривиальные конечные порядка 1 абелевы группы: 0 = ({0};+) - аддитивная, Å = ({1}; ×) - мультипликативная.
Пример 15. Легко проверить, что алгебра G = ({1; -1}; ×) является мультипликативной абелевой группой порядка 2.
Пример 16. Показать, что множество всех корней n -ой степени из 1 относительно умножения образует абелеву группу.
Доказательство. Напомним, что значения
e k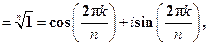 
k = 0,1,2,…, n - 1
называют корнями n-ой степени из 1. На комплексной плоскости корни n - ой степени из 1 изображаются вершинами правильного n – угольника, вписанного в окружность единичного радиуса.
Пусть e m и e s - любые корни из 1. Тогда e mn = 1 и e sn= 1,а поэтому (e m e s) n = e mn e sn = 1×1 = 1,то есть e m e s - корень n - ой степени из 1. Следовательно, умножение корней n - ой степени из1 является бинарной операцией.
Проверим выполнение аксиом G1, G2¢, второго определения группы:
G1. Так как операция умножения комплексных чисел ассоциативная, то для любых трех корней n - ой степени из 1 e m,e s,e r также выполняется условие (e m e s)e r = e m (e s e r).
G2¢. Во множестве корней n - ой степени из 1 выполнима операция деления. В самом деле, если e m и e s - любые корни n - ой степени из 1, то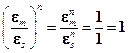 
, то есть частное 
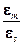есть корень n -ой степени из 1. Из коммутативности умножения комплексных чисел следует коммутативность умножения корней n - ой степени из 1: e m e s = e s e m.
Итак, алгебра (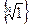
; ×) - мультипликативная абелева группа конечного порядка n.
Что требовалось доказать.
Пример 17. Так как сложение квадратных матриц n - го порядка обладает свойствами:
1) (" А, В, С Î Мn x n )[(A + B) + C = A + (B + C)];
2) ($0Î Mn x n )(" A Î Mn x n )[0 + A = A + 0 = A ];
3) (" A Î Mn x n )($(- A)Î Mn x n )[(- A) + A = A + (- A) = 0];
4) (" A, B Î Mn x n )[ A + B = B + A ],
5) множество Mn x n - бесконечное,
то алгебра M n x n = (Mn x n ; +) - аддитивная бесконечная абелева группа.
Пример 18. Доказать, что множество Z образует группу относительно действия, заданного формулой:
а * b = { a+ b,если а - четное число, b - любое целое число;
a - b,если а - нечетное число, b - любое целое число}.
Доказательство. 1. Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а поскольку как сложение, так и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.
G1. Проанализируем возможные случаи:
а) Если а, b - четные числа, а с - любое число из Z, то (а * b)* c= (a + b)+ c = a+ (b + c), a *(b * c) = a +(b + c), т.е. (a * b)* c = a *(b * c).
б) Если а - четное число, b - нечетное, а с - любое число из Z, то (a * b) * c = (a + b) - c= a + (b - c), то есть (a * b) * c = a * (b * c).
в) Если а - нечетное число, b - четное число, а с - любое число из Z, то a – b нечетно и потому (a * b) * c = (a - b) - c, a * (b * c) =
a - (b + c) = (a - b) - c, то есть (a * b) * c = a * (b * c).
г) Если а, b - нечетные числа, а с - любое число из Z, то а - b четно и потому (a * b) * c = (a - b) + c, a * (b * c) = a - (b - c) = (a-b)- c, то есть (a * b) * c = a * (b * c).
Итак, во всех возможных случаях заданная на Z бинарная операция * является ассоциативной.
G2. Так как 0 - четное число, то 0 * а= 0 + а = а. Кроме того, если а четно, то а * 0 = а + 0 = а; если же а нечетно, то а * 0 = а - 0 = а.
Итак, во всех случаях 0 * а = а * 0 = а, то есть 0 является в Z нейтральным элементом относительно заданной бинарной операции *.
G3. Для любого элемента а ÎZ в Z существует симметричный ему элемент s (a): для четного а симметричным элементом будет противоположное число - а, так как а *(-а) = а+ (- а) = 0; для нечетного а симметричным элементом будет само число а, так как
а * а = а- а= 0.
Итак, выполняются аксиомы G1-G3 и поэтому алгебра Z = (Z; *)
является группой.
В отличие от группы (Z; +) эта группа не является абелевой, поскольку не выполняется дополнительная аксиома G4. В самом деле, например, 4*5 = 4 + 5 = 9, 5*4 =5 - 4 =1, то есть 4*5 ¹ 5*4.
Что требовалось доказать.
Пример 19. Доказать, что алгебра Z m = (Z m; +), где Z m = ={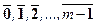 
} - множество классов вычетов по модулю m,является аддитивной абелевой группой порядка m.
|
|
|
Доказательство. Напомним, что сложение любых двух классов вычетов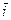 
и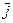 
, i, j = 0, 1, 2, …, m - 1, определяется следующим образом:
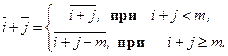
Легко доказать, что определенная таким образом сумма классов вычетов, не зависит от выбора отдельных представителей классов, используемых при составлении суммы.
Проверим для Z m справедливость условий, определяющих аддитивную абелеву группу.
Действительно, по определению сумма классов вычетов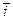 
и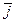 
по модулю m представляет собой единственный, вполне определенный класс вычетов по этому же модулю (замкнутость действия сложения).
G1.("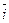 
, 
, 
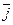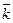ÎZ m)[( + ) + = 
+ = 
= 
=
= + 
= + ( + )]
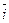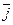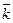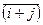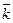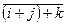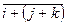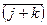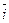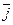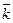(ассоциативность операции сложения).
G2. ($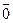 
ÎZ m)(" 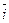ÎZ m)[ + = 
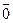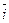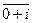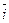= Ù + = 
= ]
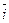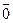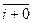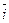(существование нулевого элемента).
G3.(" 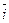ÎZ m)($(- ) = 
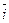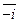ÎZ m)[(- )+ = 
+ =
= 
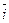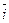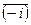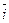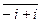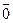= Ù + = + = 
= ]
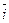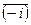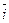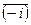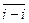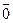(существование для каждого элемента противоположного ему).
G4. (" 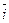, 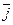ÎZ m)[ + = 
= = + ]
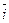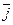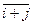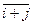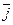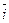(коммутативность сложения).
Отметим, что при проверке выполнимости указанных выше условий для классов вычетов, мы существенно использовали справедливость этих же условий для множества целых чисел.
Что требовалось доказать.
