Аналитическая группировка данных ‑ это деление совокупности на группы единиц по какому-либо признаку с целью выявления зависимости. Такой признак называют факторным или группировочным. Группировка позволяет оценить характер зависимости между переменными путем вычисления условного среднего.
Построение аналитических группировок проходит следующие этапы:
Ÿ выбор группировочного признака;
Ÿ определение необходимого числа групп, на которые необходимо разбить изучаемую совокупность;
Ÿ установление границ интервалов группировки;
Ÿ составление аналитической группировки.
Выбор группировочного признака является одним из существенных и сложных вопросов теории статистической группировки и статистического исследования в целом. От правильного выбора группировочного признака зависят выводы статистического исследования. В качестве основания группировки необходимо использовать признаки, наиболее полно отражающие сущность изучаемых социально-экономических явлений и процессов в условиях поставленных целей и задач.
Для целей настоящей курсовой работы в качестве группировочного признака мы выбрали X и Y.
Определение числа групп и границ интервалов было подробно рассмотрено в задании №2. После расчета этих величин можно переходить к составлению вспомогательной таблицы для аналитической группировки (табл. 5).
Таблица 5
Вспомогательная таблица для аналитической группировки
| Номер группы | Группы по факторному признаку | Номер единицы совокупности, попавшей в интервал | 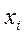
| 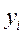
|
[ 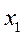 ; ; 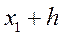 ] ]
| 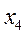
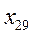
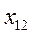
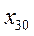
| 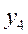
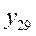
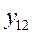
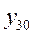
| ||
| Итого | 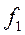 =4 =4
| S 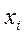
| S 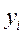
| |
| … | … | … | … | … |
| Итого | 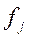
| S 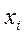
| S 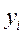
| |
| m | [ 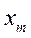 ; ; 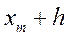 ] ]
| 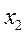
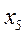
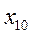
| 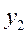
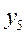
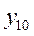
| |
| Итого | 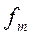 =3 =3
| S 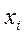
| S 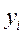
| |
| Всего | N | 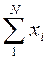
| 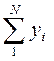
|
По каждой группе (интервалу) в этой таблице необходимо отметить номера единиц совокупности, попадающих в указанный интервал, а также выписать соответствующие им значения факторного (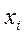 ) и результативного (
) и результативного (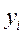 ) признаков. После чего производится расчет суммарных показателей по каждой группе: количество единиц в группе (
) признаков. После чего производится расчет суммарных показателей по каждой группе: количество единиц в группе (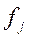 ), суммарное значение факторного признака (S
), суммарное значение факторного признака (S 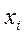 ) и суммарное значение результативного признака (S
) и суммарное значение результативного признака (S 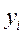 ).
).
Для установления наличия связи на основе данных вспомогательной таблицы построим итоговую аналитическую группировку. Для чего перейдем от суммарных показателей по группам к средним величинам (табл. 6).
Таблица 6
Аналитическая группировка
| № п/п | Группы по факторному признаку | Частота | Х | Y | ||
Сумма по группе
S 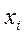
| Групповая средняя
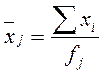
| Сумма
по группе
S 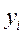
| Групповая средняя
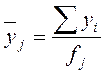
| |||
| … m | [ 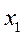 ; ; 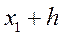 ]
…
[ ]
…
[ 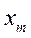 ; ; 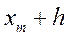 ] ]
| 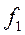 …
…
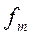
| ||||
| Итого | N | 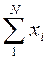
| 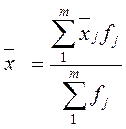
| 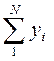
| 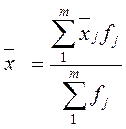
|
Групповые средние по факторному признаку в этой таблице расположены в порядке возрастания. Как же ведет себя результативный признак при увеличении факторного? Если также растет, то налицо прямая зависимость между признаками. Если убывает, то связь – обратная. Если тенденция не видна, т.е. групповые средние по результативному признаку померено увеличиваются и уменьшаются, то однозначного вывода о наличии зависимости сделать нельзя.
Приведем пример. Пусть составлена следующая аналитическая группировка для выявления зависимости суммы выданных кредитов от размера процентной ставки (табл. 7).
Таблица 7
Зависимость суммы выданных кредитов от размера процентной ставки
| № п/п | Группы банков по величине процентной ставки | Число банков | Процентная ставка | Сумма выданных кредитов, млн руб. | ||
| всего | средняя процентная ставка | всего | в среднем на один банк | |||
| 11 – 14 14 – 17 17 – 20 20 – 23 23 - 26 | 50,7 108,8 179,7 126,8 73,6 | 12,7 15,5 18,0 21,1 24,5 | 103,5 134,75 127,32 42,75 6,75 | 25,9 19,25 12,73 7,1 2,25 | ||
| Итого | 539,6 | 18,0 | 415,07 | 13,8 |
Мы видим, что по мере возрастания средней процентной ставки (12,7; 15,5; 18,0; 21,1; 24,5) происходит снижение средней суммы выданных,кредитов (25,9; 19,25; 12,73; 7,1; 2,25), а значит, налицо обратная зависимость между этими показателями.
 2015-05-20
2015-05-20 425
425








