Поле корреляции ‑ это поле точек, на котором каждая точка соответствует единице совокупности; ее координаты определяются значениями признаков х и у.
Для построения корреляционного поля используют неупорядоченные данные. На рис. 6 представлены основные типы корреляции между двумя переменными.
По характеру расположения точек на поле корреляции делают вывод о наличии или отсутствии связи, о характере связи (линейная или нелинейная, прямая или обратная).
В некоторых случаях зависимость между признаками проявляется сильнее при нанесении линии эмпирической регрессии, построенной по сгруппированным данным.

Рис. 6. Основные типы корреляции
Для этого необходимо использовать данные аналитической группировки (Задание 4, табл. 6). По оси Х откладываются интервалы и отмечаются середины интервалов (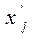 ). Затем для каждого интервала строится точка с координатами (
). Затем для каждого интервала строится точка с координатами (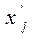 ;
;  ), где
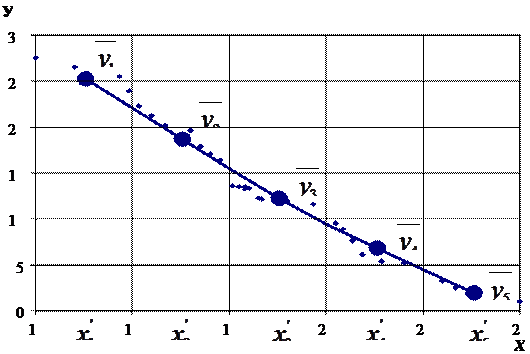
), где  ‑ групповые средние значения y из аналитической группировки. После чего построенные точки соединяются прямыми отрезками. Полученный график и будет эмпирической линией регрессии (рис. 7).
‑ групповые средние значения y из аналитической группировки. После чего построенные точки соединяются прямыми отрезками. Полученный график и будет эмпирической линией регрессии (рис. 7).
 |
Поскольку объекты в составе выборочной совокупности считаются независимыми, точки на графике не соединяют линями.
Рис. 7.Поле корреляции и эмпирическая регрессия
По внешнему виду графика можно выявить возможный характер взаимосвязи между признаками и оценить погрешность построения уравнения регрессии.
 2015-05-20
2015-05-20 426
426








