Методика решения

Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента:

1. Показатель времени, за который или по состоянию на который приводятся числовые значения (t);

2. Числовые значения того или иного показателя, называемые уровнями ряда (y).

Обычно выделяют три компонента ряда динамики: тренд, сезонные колебания и случайную составляющую. Нахождение математического выражения основной тенденции ряда динамики (тренда) осуществляется аналогично построению уравнения регрессии для рядов распределения. Однако в некоторых случаях колеблемость значений исследуемого показателя во времени настолько велика, что обосновать форму кривой очень сложно (рис. 10).

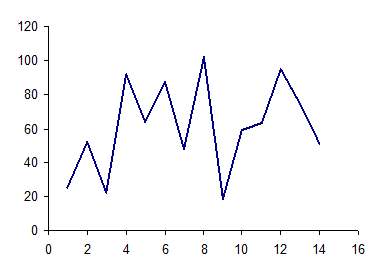
Рис. 10. Графическое изображение ряда динамики

с резкими колебаниями

В таких случаях для выделения основной тенденции используют метод скользящих средних. Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды.

Скользящие средние представляют собой средние уровни за определенные периоды времени (3, 5, 7 дней, месяцев, лет) путем последовательного передвижения начала периода на единицу времени.

Усреднение на небольшом интервале удаляет случайную составляющую. Усреднение на длительном интервале (12 месяцев) удаляет и случайную составляющую, и сезонные колебания.

Трехчленная скользящая средняя вычисляется по формуле

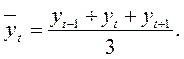
Приведем пример расчета трехчленных скользящих средних на основе данных о производстве продукции по годам (табл. 8)

Таблица 8

Производство продукции (млн шт.)

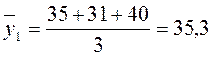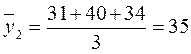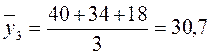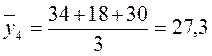; ; ; и т.д.

Мы видим, что при расчете скользящих средних необходимо последовательно сдвигать начало периода скольжения на один год (день, месяц).

После нахождения значений скользящих средних нам необходимо построить новый, сглаженный ряд динамики. Для этого каждую из скользящих средних мы закрепляем за серединой того периода, для которого она была рассчитана. Так, 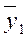- это средний объем производства за три года: 1998, 1999, 2000. Серединой первого периода скольжения является 1999 г. Поэтому 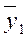записываем как сглаженный объем производства продукции в 1999 г., 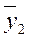‑ объем производства в 2000 г. и т.д. (табл. 9).

Таблица 9

Ряд динамики, сглаженный с помощью трехчленной скользящей средней


-	35,3	35,0	30,7	27,3	27,3	34,7	34,3	36,3	-

Как видно из табл. 9, трехчленная скользящая средняя демонстрирует выровненный динамический ряд с разнонаправленной тенденцией движения уровней: снижение до 2002 г. и далее рост их с некоторым нарушением в 2005 г. Чтобы исправить это нарушение закономерности, можно попытаться увеличить период скольжения до 5:

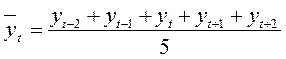Таблица 10

Ряд динамики, сглаженный с помощью пятичленной скользящей средней


-	-	31,6	30,6	31,2	31,2	30,2	34,6	-	-

Однако в нашем примере увеличение периода скольжения не дало положительных результатов. Трехчленная скользящая средняя дает более сглаженный ряд, чем пятичленная.

Поскольку укрупнение интервала сглаживания приводит к уменьшению числа сглаженных уровней ряда, а длина динамического ряда в экономике часто ограничена (максимум 10-15 лет), то многочленные скользящие средние практически не применяются (исключение составляет применение 12-членных скользящих средних для устранения сезонных колебаний).

Простые скользящие средние в ряде случаев позволяют выявить тенденцию лишь в общих чертах, ибо при сглаживании исчезают изгибы линии тенденции и некоторые уровни показывают вместо спада, имевшего место реально, подъем или наоборот (см., например, табл. 11 - 2005, 2006 гг.).

Более совершенным приемом считается взвешенная скользящая средняя. Если при простой скользящей средней все уровни временного ряда считаются равноценными, то при исчислении взвешенной скользящей средней каждому уровню в пределах интервала сглаживания приписывается вес, зависящий от расстояния данного уровня до середины интервала сглаживания.

Веса для уровней ряда при сглаживании могут быть взяты как коэффициенты бинома Ньютона:

Интервал сглаживания (n)	Коэффициенты (f)	Сумма весов
	1 2 1
	1 4 6 4 1
	1 6 15 20 15 6 1

Взвешенная скользящая средняя определяется как средняя арифметическая взвешенная:

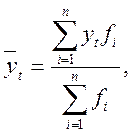
где 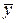‑ скользящая средняя; y_t ‑ уровни динамического ряда, участвующие в расчете за интервал n; f_i ‑ веса.

Для рассматриваемого примера трехчленная взвешенная скользящая средняя за 1999 г. окажется равной

;

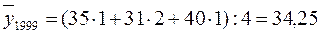для 2000 г. соответственно получим

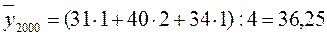При пятичленной взвешенной скользящей средней для 2000 и 2001 гг.получим

;

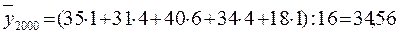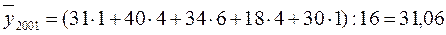Аналогично рассчитываются и для других лет взвешенные скользящие средние, результаты которых приведены в табл. 11.

Таблица 11

Годы	Фактический уровень,	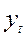Сглаженные уровни
Простая скользящая средняя	Взвешенная скользящая средняя
3-членная	5-членная	3-членная	5-членная
		-	-	-	-
		35,3	-	34,3	-
		35,0	31,6	36,3	34,6
		30,7	30,6	31,5	31,1
		27,3	31,2	25.0	27,4
		27,3	31,2	28,0	28,9
		34,7	30,2	34,5	29,4
		34,3	34,6	35,8	35,1
		36,3	-	34,5	-
		-	-	-	-
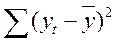		234,43	365,4	136,81	215,87

Для того, чтобы определить, какой из методов сглаживания дает меньшую погрешность, необходимо рассчитать сумму квадратов отклонений фактический значений ряда от их сглаженных значений - 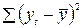. Чем меньше полученная величина, тем точнее сглаженный ряд описывает исходные данные. Так, для нашего примера оптимальным является сглаживание по методу трехчленной взвешенной скользящей средней.

При сглаживании ряда динамики по чётному числу возникает вопрос: к какому периоду относить скользящую среднюю (например, ко второму или к третьему уровню для четырехчленной скользящей средней (рис. 11)). Для решения этой проблемы существует процедура центрирования, т.е. нахождение средней величины на основе двух скользящих средних.

На рис. 11 наглядно видно, если нецентрированная средняя 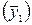формально относится к середине между 2-м и 3-м уровнем, то центрированную скользящую среднюю 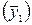можно абсолютно оправданно присвоить третьему периоду.

Если исчисляется скользящая средняя с продолжительностью периода, равной 2, то расчет производится следующим образом.

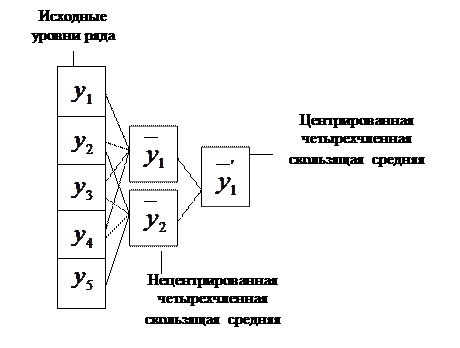Рис. 11. Графическое представление нахождения

центрированной четырехчленной скользящей средней

Нецентрированные скользящие средние:

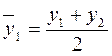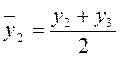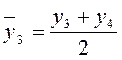; ; и т.д.

Центрированные средние:

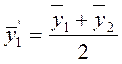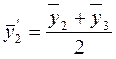; и т.д.

Расчет четырехчленной скользящей средней ведется аналогичным образом.

Нецентрированные скользящие средние:

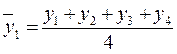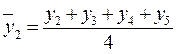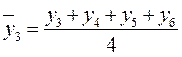; ; и т.д.

Центрированные средние:

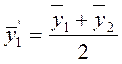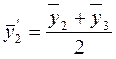; и т.д.

Рассчитаем двухчленные и четырехчленные скользящие средние по данным нашего примера (табл. 12, 13).

Таблица 12

Годы	Фактический уровень,	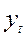Двухчленная скользящая средняя
Нецентрированная	Центрированная
			-
		40,5	39,25
			38,75
			31,5


			34,5
		34,5	35,75
		34,5	34,5
		-	-
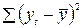			112,44

Таблица 13

Годы	Фактический уровень,	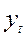Четырехчленная скользящая средняя
Нецентрированная	Центрированная
		-	-
		37,5	-
		33,25	35,38
		30,5	31,88
			29,75
		30,5	29,75
		33,25	31,88
		35,75	34,50
		-	-
		-	-
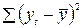			198,71