Выборочное среднее значение 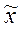 , вычисляемое по выборке ограниченного объема n, будет отличаться от идеального «точного» значения
, вычисляемое по выборке ограниченного объема n, будет отличаться от идеального «точного» значения 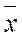 , которое можно было бы получить для бесконечно большой выборки. Разница между выборочным средним и генеральным средним называется предельной ошибкой выборки:
, которое можно было бы получить для бесконечно большой выборки. Разница между выборочным средним и генеральным средним называется предельной ошибкой выборки:
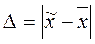 .
.
Поскольку среднее значение генеральной совокупности (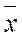 ) обычно неизвестно, а задача заключается именно в его нахождении, существует следующая процедура для расчета предельной ошибки выборки.
) обычно неизвестно, а задача заключается именно в его нахождении, существует следующая процедура для расчета предельной ошибки выборки.
Сначала определяется средняя ошибка выборки (μ):
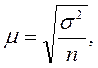
где 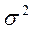 ‑ дисперсия признака в генеральной совокупности; п ‑ объем выборочной совокупности.
‑ дисперсия признака в генеральной совокупности; п ‑ объем выборочной совокупности.
Такая формула применяется для повторной выборки. При повторном отборепопавшая в выборку единица подвергается обследованию, а затем возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Тем самым вероятность попадания каждой отдельной единицы в выборку остается постоянной на всем протяжении отбора.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Поэтому вероятность попасть в выборку для оставшихся единиц увеличивается с каждым шагом отбора.
В случае расчета средней ошибки бесповторной выборки применяется скорректированная формула:
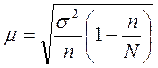 ,
,
где N – численность генеральной совокупности. Величина (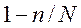 ) всегда меньше единицы, поэтому сопоставление приведенных формул свидетельствует о том, что применение бесповторного отбора обеспечивает меньшую ошибку выборки.
) всегда меньше единицы, поэтому сопоставление приведенных формул свидетельствует о том, что применение бесповторного отбора обеспечивает меньшую ошибку выборки.
Обычно, если объем выборки не превышает 5 % генеральной совокупности, к формуле для бесповторного отбора можно не переходить.
На практике величина дисперсии признака в генеральной совокупности (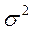 ), как правило, неизвестна, поэтому ее заменяют выборочной дисперсией (
), как правило, неизвестна, поэтому ее заменяют выборочной дисперсией (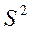 ). Это возможно, поскольку доказано, что соотношение
). Это возможно, поскольку доказано, что соотношение 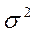 и
и 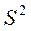 определяется равенством
определяется равенством

При большой численности выборочной совокупности сомножитель (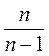 ) стремится к единице и им можно пренебречь.
) стремится к единице и им можно пренебречь.
После нахождения средней ошибки выборки (μ) можно переходить к оценке предельной ошибки (Δ), используя следующую формулу:
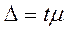 ,
,
где t – коэффициент доверия, показывающий, во сколько раз необходимо увеличить среднюю ошибку выборки, чтобы с заданным уровнем вероятности утверждать, что разница между выборочной и генеральной средними не превысит предельной ошибки выборки.
Коэффициент доверия t определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности.
Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие им значения t.
| P(t) | 0,683 | 0,9 | 0,950 | 0,954 | 0,990 | 0,997 |
| t | 1,00 | 1,64 | 1,96 | 2,00 | 2,58 | 3,00 |
Проявление ошибки большей, чем утроенная средняя ошибка выборки, имеет крайне малую вероятность (1 – 0,997 = 0,003 или 0,3 %) и считается практически невозможным событием. Такой уровень доверительной вероятности применяется для расчетов, требующих особенной точности. В большинстве случаев достаточными являются 90 % и 95 % вероятность.
Зная величину выборочной средней (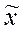 ) и предельную ошибку выборки (
) и предельную ошибку выборки (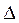 ), можно определить доверительные интервалы, в которых с заданным уровнем вероятности находится значение генеральной средней:
), можно определить доверительные интервалы, в которых с заданным уровнем вероятности находится значение генеральной средней:
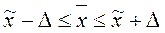 .
.
 2015-05-20
2015-05-20 357
357








