Методика решения

Параметры линейного уравнения парной регрессии 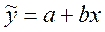находятся методом наименьших квадратов (МНК). Исходное условие МНК формулируется следующим образом:

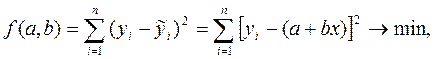
т.е. должна быть обеспечена минимальность суммы квадратов отклонений фактических значений результативной переменной (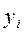) от ее теоретических значений (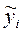), получаемых на основе уравнения регрессии ().

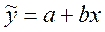Для отыскания значений параметров а и b, при которых f(a,b) принимает минимальное значение, приравниваем нулю первые частные производные функции:

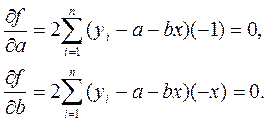
Преобразуя полученные уравнения, получаем систему нормальных уравнений МНК для прямой:

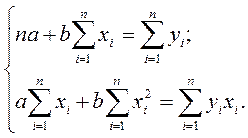
Решая систему, получаем оценки неизвестных коэффициентов a и b:

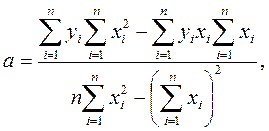
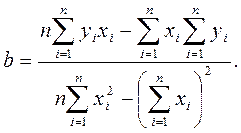
Можно найти параметр а, разделив на n первое уравнение системы:

,

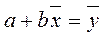отсюда

.

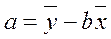Параметр b может быть выражен следующим образом:

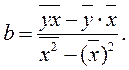
Так как знаменатель этого выражения есть не что иное, как дисперсия переменной x, формула коэффициента регрессии b может быть записана следующим образом:

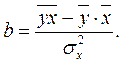
Найденные параметры а и b подставляем в исходное уравнение 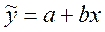и получаем уравнение регрессии.