Линия тока

Если через ряд точек потока жидкости провести кривую таким образом, что вектор скорости частицы жидкости в каждой точке будет касательным к этой кривой (рис. 3.1), то такая линия, характеризующая направление движения ряда последовательно расположенных частиц жидкости в данный момент времени, называется линией тока.

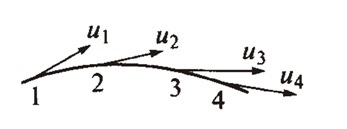
Рисунок 3.1 - Линия тока

При установившемся движении линия тока и траектория частицы жидкости совпадают. При неустановившемся движении линии тока не будут совпадать с траекториями частиц жидкости, так как направление и величина скоростей отдельных частиц жидкости с течением времени будут меняться и частицы жидкости, находившиеся в какой-то момент времени на одной линии тока, в следующий момент окажутся на разных.

Рассмотрим движение частицы жидкости (рис. 3.2).

За момент времени 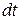частица при скорости 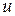пройдет некоторый путь 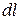, проекции которого на координатные оси будут 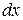, , 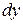, 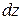а составляющие скорости:

; ; ,

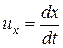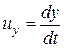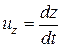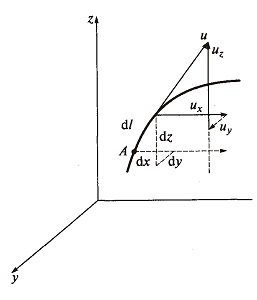
Рисунок 3.2 Составляющие скорости течения потока в точке

откуда получим:

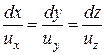. (3.3)

Это уравнение называется уравнением линии тока.