2015-05-20
1067
Если в движущейся жидкости выделить в плоскости, перпендикулярной течению, элементарную бесконечно малую площадку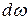 
(рис. 3.3) и через все точки, находящиеся на ее контуре, провести линии тока для данного момента времени, то получившаяся поверхность называется трубкой тока, а находящаяся в ней жидкость образует элементарную струйку, которая обладает следующими свойствами:
- форма элементарной струйки при установившемся движении остается неизменной во времени, так как в этом случае линии тока с течением времени не меняют своей формы;
- вхождения в элементарную струйку внешних линий тока и выхода из нее содержащихся в ней линий тока не происходит, так как боковая поверхность элементарной струйки образована линиями тока, к которым скорости направлены по касательной;
- скорости во всех точках поперечного сечения элементарной струйки можно считать одинаковыми вследствие незначительности поперечного сечения элементарной струйки.
Рассмотрим элементарную струйку потока с поперечным сечением 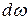(см. рис. 3.3) и постоянной скоростью движения частиц 
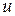по сечению струйки.
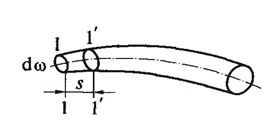
Рисунок 3.3 Элементарная струйка
Через промежуток времени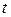 
частицы жидкости из поперечного сечения 1 - 1 переместятся в сечение 1` - 1` на расстояние s; при этом через сечение 1 - 1 пройдет элементарный объем жидкости 
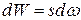. Разделив обе части равенства на промежуток времени 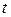, получим
,
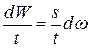где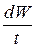 
- элементарный объем, прошедший через сечение 1 - 1 за единицу времени, т.е. элементарный расход струйки 
;
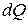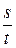- путь, пройденный за единицу времени, т.е. скорость движения жидкости .
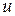Таким образом,
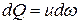, (3.4)
т. е. расход струйки равен произведению площади ее поперечного сечения на скорость в этом сечении.
