Задача 1. Доказать, что отрезок, соединяющий середины противоположных ребер правильного тетраэдра, есть общий перпендикуляр этих ребер.
Решение
Пусть ребро тетраэдра равно а. Введем векторы 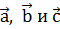 и MN (рис. 8). Пользуясь определением разности векторов, запишем:
и MN (рис. 8). Пользуясь определением разности векторов, запишем: 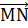 =
= 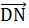 -
- 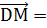
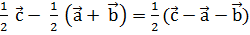 . Найдем скалярное произведение векторов:
. Найдем скалярное произведение векторов: 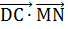 =
= 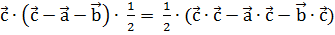 =
=  = 0
= 0
Следовательно, 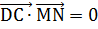 .
.
А это условие перпендикулярности векторов, т. е. DC ⊥ MN. Аналогично доказывается, что MN ⊥ АВ.
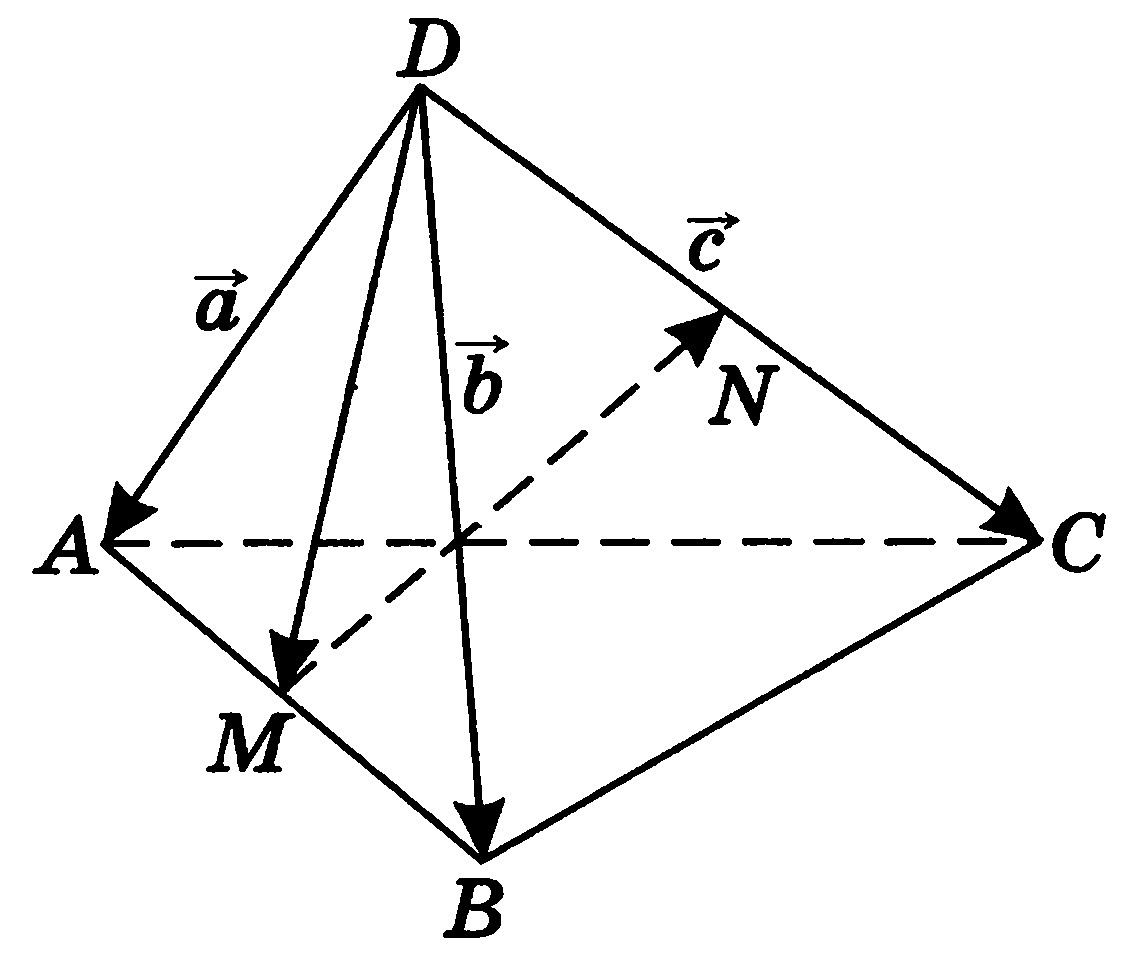
Рис. 8
Задача 2. Доказать, что если точки А, B, С, D таковы, что AB ⊥ CD,
AC ⊥ BD, то AD ⊥ BC.
Доказательство
Введем обозначения (рис. 9): 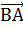 =
= 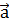 ,
, 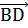 =
= 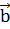 ,
, 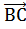 =
=  . Тогда
. Тогда 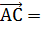
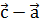 ,
,
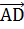 =
= 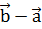 ,
, 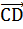 =
= 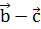 . Так как по условию
. Так как по условию 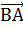 ⊥
⊥ 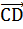 и
и 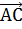 ⊥
⊥ 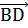 , то
, то
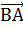

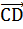 = 0 и
= 0 и 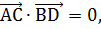 т. е.
т. е. 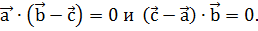
Раскрывая скобки и складывая почленно два полученных равенства, получаем 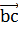 -
- 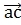 = 0. Тогда
= 0. Тогда 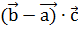 = 0, т. е.
= 0, т. е. 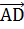

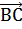 = 0, а это на векторном языке означает, что AD ⊥ ВС.
= 0, а это на векторном языке означает, что AD ⊥ ВС.
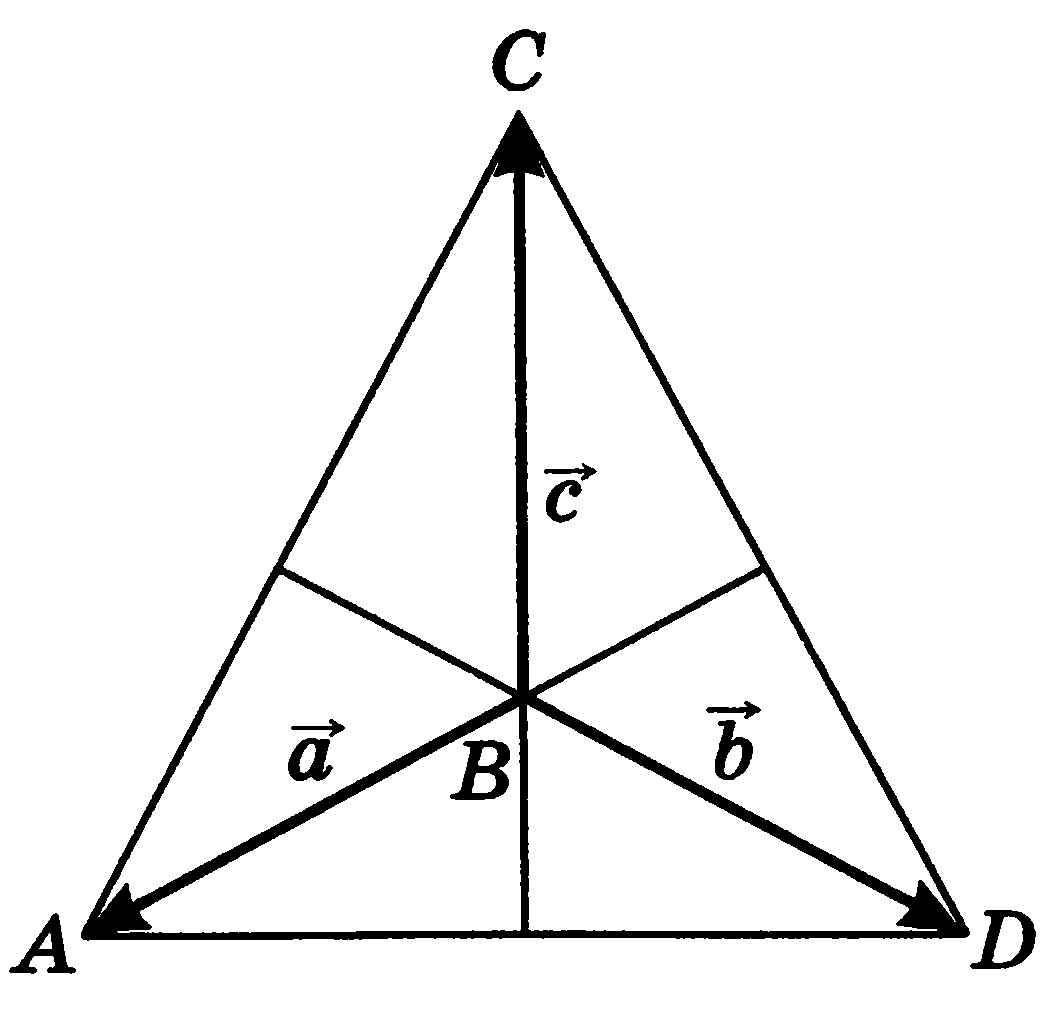
Рис. 9
 2015-05-20
2015-05-20 1302
1302








