Задача 1. Доказать, что сумма расстояний от любой точки, взятой внутри правильного треугольника, до стороны этого треугольника есть величина постоянная для данного треугольника.
Доказательство
Пусть внутри правильного треугольника ABC (рис. 12) взята произвольно точка М и расстояния от точки М до сторон треугольника АВ, АС, ВС соответственно  равны
равны 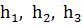 .
.
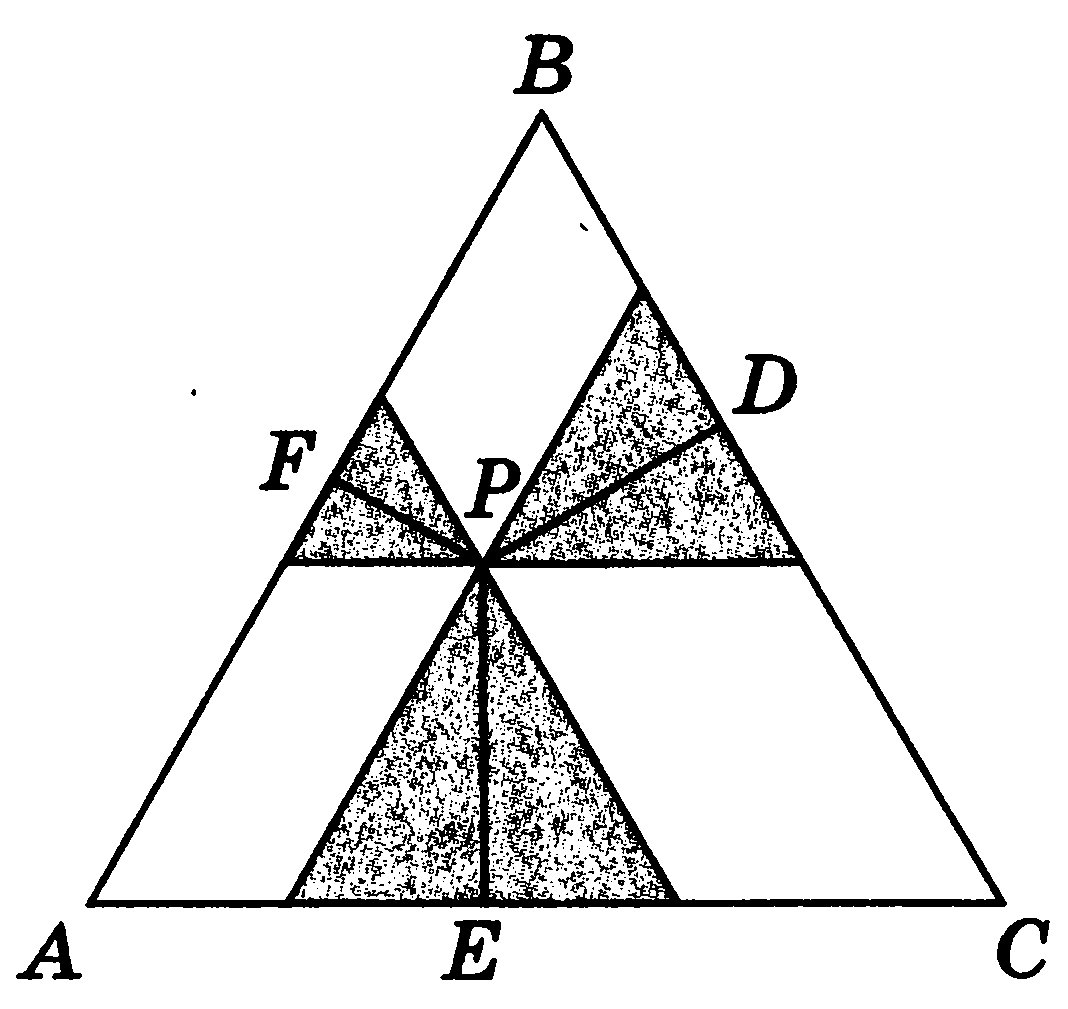
Рис. 12
Соединив точку М с вершинами треугольника АВС, разобьем его на три треугольника. Тогда площадь ∆АВС будет равна сумме площадей этих треугольников, т. е. 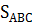 =
= 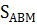 +
+ 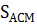 +
+ 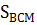 .
.
Обозначим длину стороны треугольника через а и длину его высоты через h. Получим 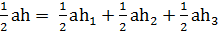 .
.
Отсюда 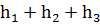 = h, т. е. сумма расстояний от точки М до сторон
= h, т. е. сумма расстояний от точки М до сторон
равностороннего треугольника ABC есть величина постоянная, равная высоте треугольника. Покажем, как можно решить эту же задачу иначе.
Пусть внутри равностороннего треугольника ABC взята произвольная точка Р (рис. 12), из которой опущены перпендикуляры PD, РЕ и PF соответственно на ВС, СА и АВ.
Проведем через точку Р три прямые, параллельные сторонам треугольника ABC. Три образовавшихся треугольника (они на рисунке закрашены) также равносторонние, и сумма длин их сторон равна сумме длин сторон треугольника ABC. Значит, и сумма длин их высот равна длине высоты треугольника ABC, которая есть константа.
Заметим, что эта задача может быть обобщена на случай любого выпуклого правильного многоугольника.
Пусть сторона многоугольника равна а, расстояния от точки М до сторон многоугольника равны 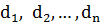 . Соединив точку М с вершинами многоугольника, разобьем его на n треугольников. Сумма их площадей равна площади многоугольника, которая при заданном многоугольнике есть величина постоянная:
. Соединив точку М с вершинами многоугольника, разобьем его на n треугольников. Сумма их площадей равна площади многоугольника, которая при заданном многоугольнике есть величина постоянная: 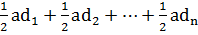 = S.Преобразовав равенство, получим
= S.Преобразовав равенство, получим 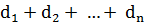 . =
. = 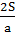 = const.
= const.
Задача 2. Стороны а, b, с треугольника ABC (рис. 13) лежат соответственно против углов А, B, С. Доказать, что биссектриса угла А вычисляется по формуле l = 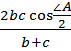 .
.
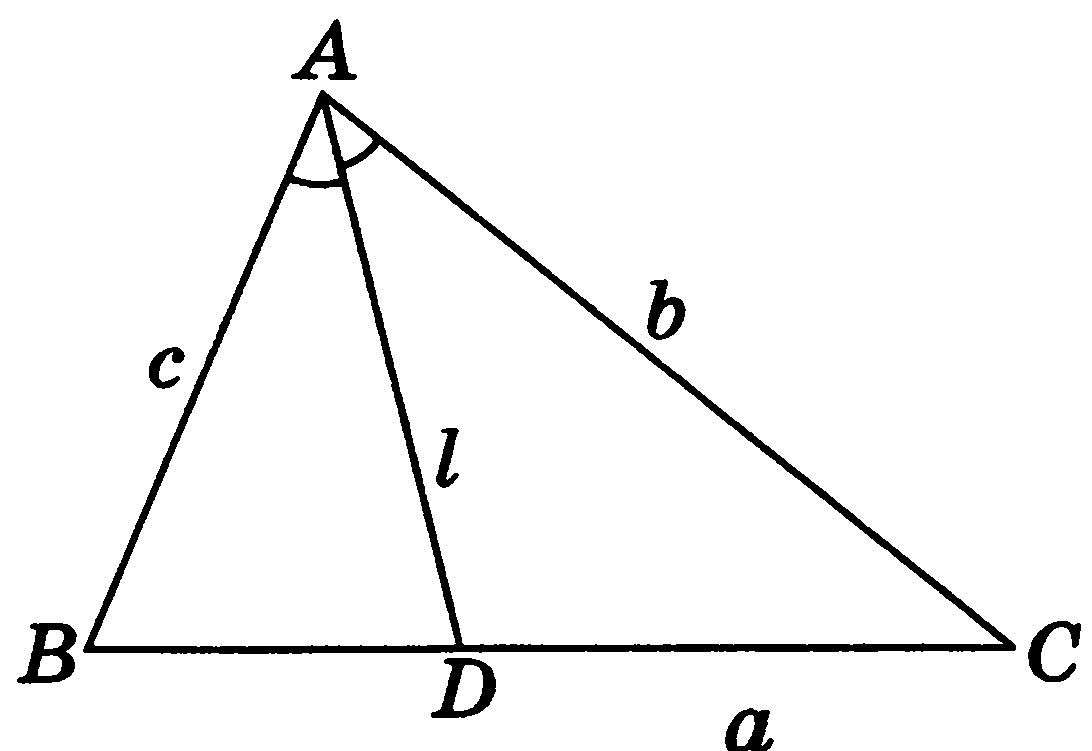
Рис. 13
Доказательство
Биссектриса AD разбивает треугольник ABC на два треугольника: ADB и ADC. Тогда 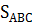 =
= 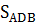 +
+ 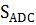 . Это означает, что
. Это означает, что 
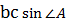 =
=  cl sin
cl sin 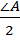 +
+
+  bl sin
bl sin 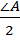 . Учитывая также, что
. Учитывая также, что  = 2 sin
= 2 sin 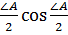 , получаем
, получаем
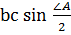
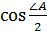 =
=  cl sin
cl sin  bl sin
bl sin 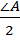 . Отсюда bс
. Отсюда bс 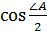 =
=  (c+ b)l, тогда
(c+ b)l, тогда
l = 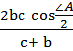 .
.
 2015-05-20
2015-05-20 1603
1603








