2015-05-20
826
Задача 1. Доказать, что сумма расстояний от произвольно взятой внутри треугольника ABC точки О до вершин треугольника больше его полупериметра.
Доказательство
Рассмотрим треугольники АОВ, ВОС, СОА (рис. 15).
Используя неравенство треугольника, запишем три неравенства:
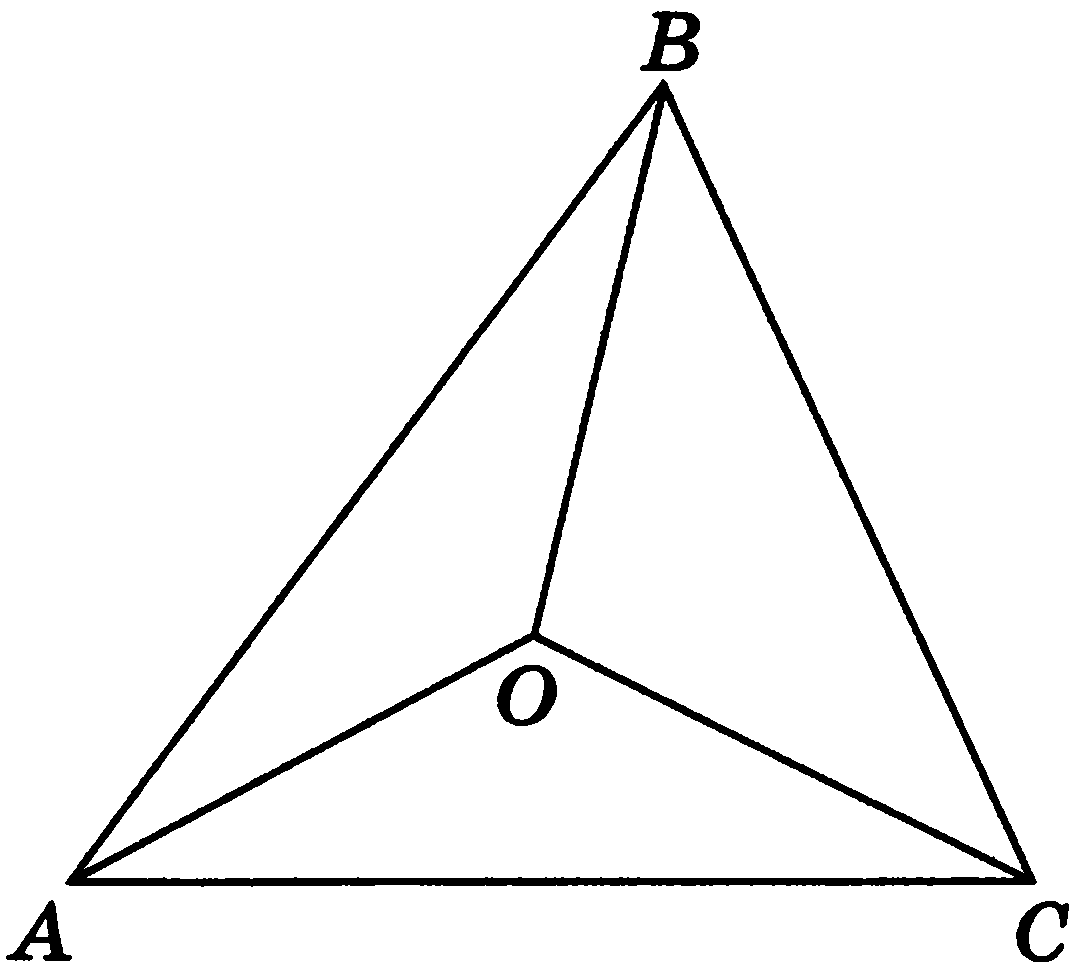
Рис. 15
АО + О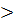В 
АВ,
ВО + ОО 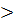ВС,
АО + ОО 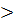АС.
Сложим почленно эти три неравенства: 2 
AO + 2 BO + 2 CO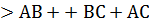 
.
Разделив обе части неравенства на 2, мы получим доказываемое
неравенство: AO + BO + CO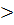 
(
).
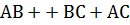Задача 2. Доказать, что медиана треугольника меньше полусуммы заключающих ее сторон.
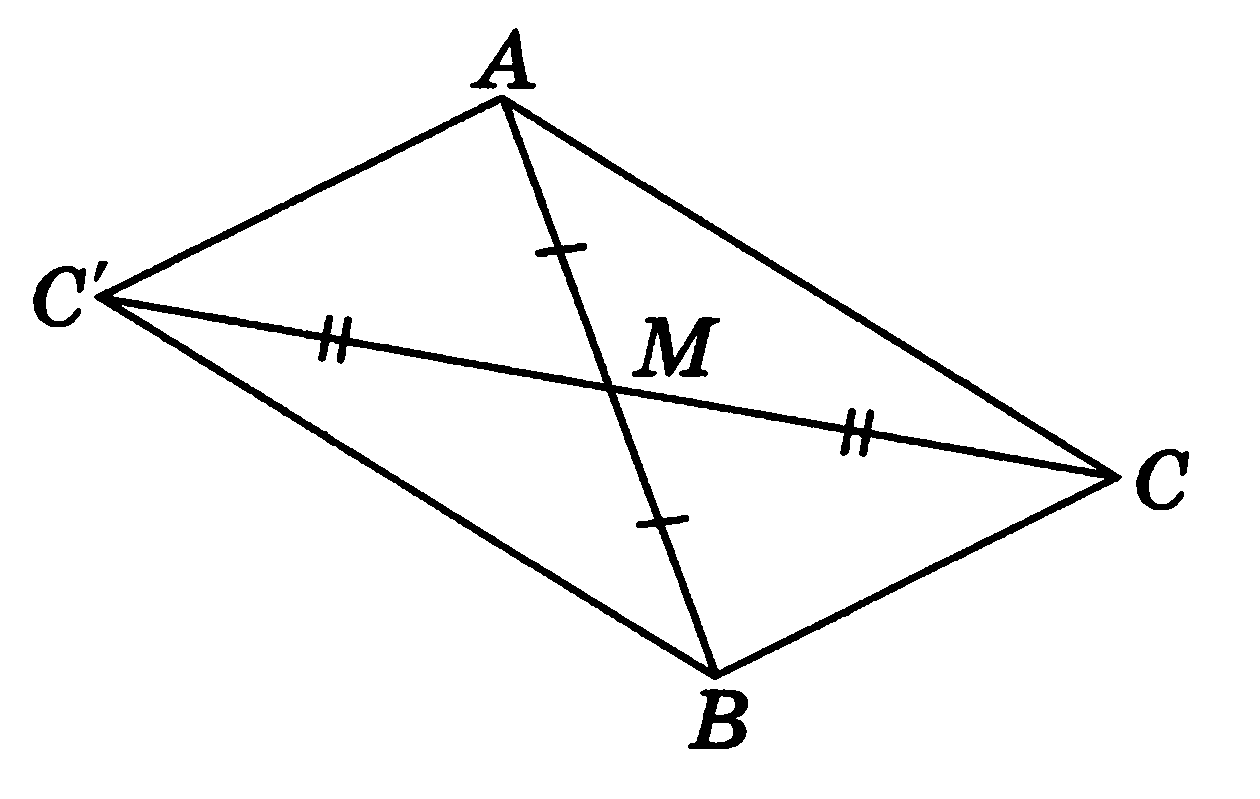
Рис. 16
Доказательство
Пусть СМ — медиана треугольника ABC (рис. 16). Продолжим МС на отрезок МС' = СМ. Тогда четырехугольник АСВС'— параллелограмм, и, следовательно, ВС'=АС, СС' = 2 СМ. Используя неравенство треугольника, получаем: СВ + АС, откуда СМ < (АС + СВ).
