Алгебраический метод

(Метод, основанный на решении уравнений).

Задача 1. В равнобедренной трапеции отношение оснований равно 0,75; средняя линия трапеции равна высоте h и равна 7 см. Доказать, что радиус окружности, описанной около трапеции, равен 5 см.

Решение

По условию задачи отношение оснований 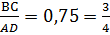. Обозначая AD = 4x, ВС = Зx и зная длину средней линии трапеции, имеем 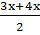= 7, откуда находим х = 2, т.е. основания трапеции ВС = 6 см, AD = 8 см.

Центр О описанной окружности лежит на высоте трапеции, проведенной через точку пересечения диагоналей. Обозначим искомый радиус окружности через R, отрезок ON через z тогда OM=7- z.

Из прямоугольных треугольников AON и ВОМ (рис. 17) находим по теореме Пифагора: , .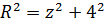

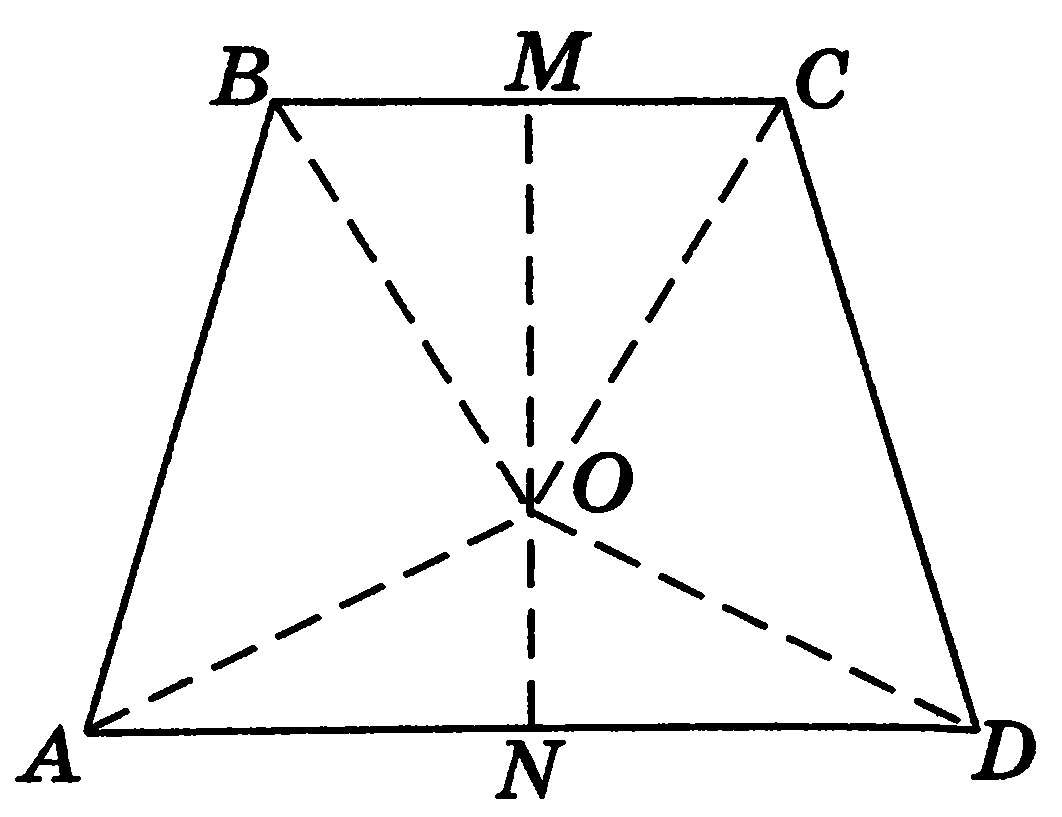
Рис. 17

Имеем систему

Решая систему, получим z = 3, R = 5.

Итак, радиус описанной окружности равен 5 см.

Задача 2. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Доказать, что большая сторона на 8 см больше меньшей стороны.

Решение

Если обозначить расстояние от точки пересечения диагоналей до большей стороны через х, то запись решения будет наглядной (рис. 18) и очень компактной:

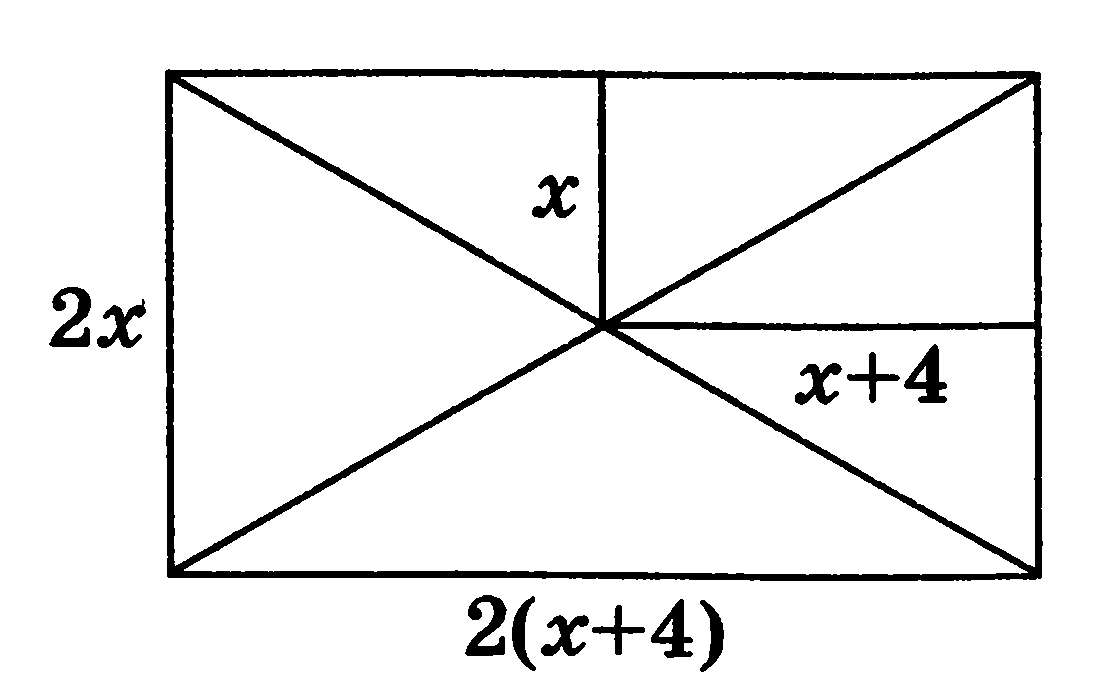
Рис.18

2x + 2(x + 4) = 28,

4х = 20,

x = 5.

Большая сторона равна 18 см, а меньшая — 10 см, а это и доказывает, что большая сторона на 8 см длиннее меньшей стороны.

Задача 3. Трапеция разбита на параллелограмм и треугольник, которые равновелики (рис. 19). Чему равно большее основание трапеции, если меньшее равно 3 см?

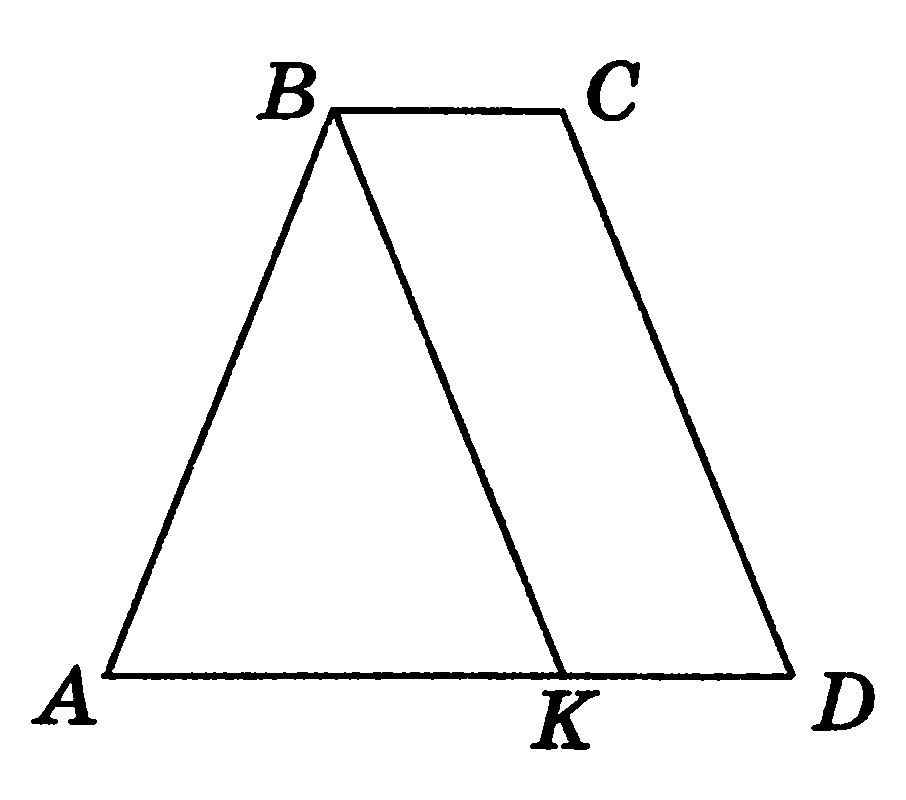
Рис.19

Решение

Согласно условию задачи имеем 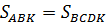(1)

Если обозначить отрезок АК через х, то площадь треугольника АВК можно выразить равенством 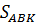= xh, где h — высота треугольника АВК.

Если учесть, что высота параллелограмма BCDK такая же, как и у треугольника АВК, то его площадь можно выразить равенством 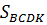= KD h = 3 h. Согласно равенству (1) имеем уравнение xh = 3h, откуда