2015-05-20
325
Глава 1. ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
Обозначения: E 2={0,1}; Е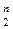 
= E 2´ E 2´...´ E 2 – прямое произведение n сомножителей; (x 
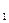,.., xn) Î 
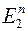, | E 2| – мощность E 2, | E 2|=2, тогда | Е 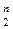|=2 n.
Определение. Функцией алгебры логики называется отображение Е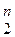 
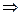E2, причем отображение всюду определено и функционально.
Так как множество Е 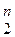конечно, то задать отображение Е 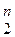Þ E 2 означает задать множество наборов из Е 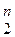и для каждого набора указать его образ в Е 2.
Пример 1. Пусть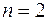 
, тогда Е 
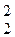= {(0 0), (0 1), (1 0), (1 1)},
отображение Е 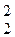Þ E 2 задано, например, так: (0 0) Þ0; (0 1) Þ1; (1 0) Þ1; (1 1) Þ1. Тем самым задана функция, для которой мы будем использовать стандартное обозначение f (x 1, x 2), записывая эту функцию в виде табл. 1.
Таблица 1
| x 1 | x 2 | f (x 1, x 2) |
Здесь x 1 и x 2 обозначают названия столбцов, а f – символ, обозначающий отображение. Следует обратить внимание, что функции
f (x 1, x 2) и f (y 1, y 2) задают одно и то же отображение и их таблицы отличаются только названиями столбцов.
Определение. Таблица, задающая функцию f(x1,x2,...,xn), называется таблицей истинности для этой функции.
Рассмотрим функции одной переменной. Их будет всего 4, они задаются таблицами истинности 2–5:
Таблица 2
| x | f 0(x) |
Функция называется константой 0, записывается f 0(x)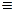 
0.
Таблица 3
| x | f 1(x) |
Функция называется тождественной, записывается f 1(x)= x.
Таблица 4
| x | f 2(x) |
Функция называется «не x» и записывается f 2 (x)=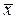 
.
Таблица 5
| x | f 3(x) |
Функция записывается f 3(x) 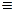1 и называется константой 1.
Если стандартным расположением переменной x считать 0 в первой строке и 1 во второй, то функции f 0, f 1, f 2, f 3 определяются однозначно наборами значений: f 0=(0,0), f 1=(0,1), f 2=(1,0) и f 3=(1,1). Наборы значений функций составляют множество E 2´ Е 2, поэтому количество функций одной переменной равно | E 2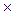 
E 2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
Рассмотрим функции двух переменных f (x 1, x 2). Функции двух переменных определены на множестве Е 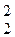={(0 0), (0 1), (1 0), (1 1)}, эти наборы переменных из Е 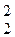можно тоже рассматривать как двоичные коды чисел 0, 1, 2, 3. Именно такой порядок расположения наборов (x 1, x 2) будем считать стандартным. Тогда функции f (x 1, x 2) определяются однозначно наборами значений (b 1, b 2, b 3, b 4), где каждое bi Î E 2, поэтому (b 1, b 2, b 3, b 4)Î Е 
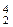. Следовательно, число функций двух переменных равно 24=16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции (табл. 6).
Таблица 6
| x 1 x 2 | f 0 | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 | f 12 | f 13 | f 14 | f 15 |
| 0 0 0 1 1 0 1 1 |
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их.
1) f 1(x 1, x 2) = (x 1& x 2), читается «конъюнкция х 1 и х 2», иногда вместо знака & употребляют знак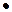 
или вообще его опускают, пишут (х 1 х 2). Конъюнкция совпадает с обычным произведением х 1 х 2 и совпадает с min(x 1, x 2). Эту операцию называют также логическим умножением.
2) f 6(x 1, x 2) = (x 1Å x 2) – сложение х 1 и х 2 по модулю два, иногда пишут (х 1+ х 2) mod 2.
3) f 7(x 1, x 2) = (x 1Ú x 2), читается «х 1 дизъюнкция х 2», она совпадает с max(x 1, x 2), ее называют логическим сложением.
4) f 8(x 1, x 2) = (x 1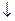 
x 2), читается «х 1 стрелка Пирса х 2» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.
5) f 9(x 1, x 2) = (x 1~ x 2), читается «х 1 эквивалентно х 2».
6) f 13(x 1, x 2) =(x 1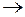 
x 2), читается «х 1 импликация х 2», иногда обозначается 
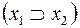, т. е. х 1 влечет х 2.
7) f 14(x 1, x 2) = (x 1| x 2), читается «х 1 штрих Шеффера х 2», она является отрицанием конъюнкции.
Cимволы 
, &, Ú,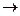 
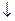, ~, , Å, |, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи», а 1 – «истине», а функции алгебры логики называются еще и булевыми функциями.
Рассмотрим функцию f (x 1... xn), где (x 1... xn)Î Е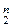 
, тогда число наборов (x 1... xn), где функция f (x 1... xn) должна быть задана, равно | Е 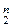|=2 n. Обозначим множество всех функций двузначной алгебры логики Р 2. Обозначим через Р 2(n) число функций, зависящих от n переменных. Очевидно, 
.
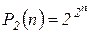С ростом n число Р 2(n) быстро растет: P 2(1)=4, P 2(2)=16, P 2(3)=256, P 2(4)=65536. При больших n табличный способ задания функций становится неприемлемым, используется формульное задание функций. Но прежде чем ввести понятие формулы, дадим определение существенной переменной.
Определение. Функция f(x1,...,xi–1,xi,xi+1,...,xn) существенно зависит от переменной хi, если существуют такие значения a1,... ai–1, ai+1,...an переменных x1,... xi–1, xi+1,... xn, что
f(a1,... ai–1, 0, ai+1... an) ¹ f(a1... ai–1, 1, ai+1... an).
Тогда переменная хi называется существенной переменной. В противном случае хi называется фиктивной переменной.
Пример 2. Рассмотрим несколько функций двух переменных (табл. 7).
Таблица 7
| x 1 | x 2 | (x 1& x 2) | f 3 | f 15 |
Покажем, что (х 1& x 2) существенно зависит от х 1. Рассмотрим наборы (0,1) и (1,1), здесь a 2=1, f (0, a 2)=0 и не равно f (1, a 2)=1. Покажем, что х 2 – тоже существенная переменная. Рассмотрим наборы (1,0) и (1,1). Здесь a 1=1, f (1,0)=0 и не равна f (1,1)=1. Для функции f 3(x 1, x 2) покажем, что х 2 – фиктивная переменная, т.е. надо показать, что не существует наборов (a 1,0) и (a 1,1) таких, что f 3(a 1,0)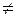 
f 3(a 1,1). Пусть a 1=0, т.е. рассмотрим наборы (0,0) и (0,1), f (0,0) = f (0,1) = 0. Пусть a 1=1, но f (1,0) = f (1,1) = 1.
Для функции f 15 x 1 и x 2 являются фиктивными переменными:
x 1 – фиктивная переменная, так как не существуют наборы (0, a 2) и (1, a 2) такие, что f (0, a 2) ¹ f (1, a 2). Если a 2 = 0, то f (0,0) = f (1,0)=1, если a 2 = 1, тогда f (0,1) = f (1,1) = 1. Аналогично доказывается, что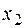 
тоже фиктивная переменная.
Пусть хi является фиктивной переменной для функции f (x 1,..., xi,..., xn). Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида (a 1,... ai– 1, 1, ai +1,... an) или, наоборот, все строки вида (a 1,..., ai– 1, 0, ai +1,... an) и столбец для переменной хi. При этом получим таблицу для некоторой функции g (x 1,..., xi –1, xi +1,... xn). Будем говорить, что функция g (x 1,... xi –1, xi +1,... xn) получена из функции f (x 1,..., x i,... xn) путем удаления фиктивной переменной хi или f получена из g путем введения фиктивной переменной хi (табл. 8).
Определение. Функции f1 и f2 называются равными, если f2 можно получить из f1 путем добавления или удаления фиктивной переменной.
