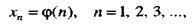2015-05-20
234
Числовой последовательностью (или последовательностью) называется функция
определенная на множестве натуральных чисел. Каждое значение хn (п= 1, 2, 3,...) называется элементом последовательности, а число п -его номером.
Числовая последовательность всегда содержит бесконечное множество элементов; среди них, конечно, могут быть и равные.
Число а называется пределом последовательности (хn), если для любого числа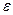 
> 0 найдется такой номер N, что при всех п > N выполняется неравенство
 |
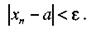Последовательность, имеющая предел, называется сходящейся, последовательность, у которой нет предела, - расходящейся.
Последовательность (хn) называется ограниченной сверху (снизу), если существует такое число А, что хп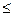 
А (соответственно хп 
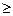А) для всех номеров п.
Последовательность (хп), ограниченная сверху и снизу, называется просто ограниченной.
