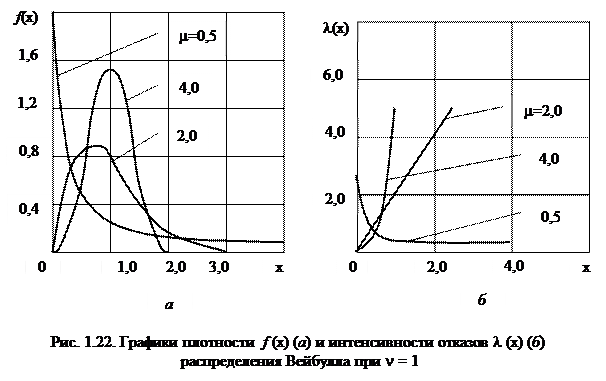
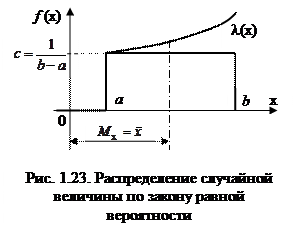
Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. Распределение по закону равной вероятности встречается, когда наряду со случайными факторами, вызывающими рассеивание, действует доминирующий систематический фактор, непрерывно и равномерно изменяющий во времени положение центра группирования M x. Графически такое распределение случайной величины отображается прямоугольником (рис. 1.23).
|
|
Если рассеяние размеров зависит только от переменных систематических погрешностей, от износа режущей кромки инструмента, то распределение действительных размеров партии деталей подчиняется закону равной вероятности.
Например, при установившемся износе режущего инструмента уменьшение его размеров во времени подчиняется прямолинейному закону, что соответственно увеличивает (при обработке валов) или уменьшает (при обработке отверстий) диаметры обрабатываемых заготовок. Тогда в момент времени t 1 вал будет иметь размер а, в момент времени t 2 - b. Естественно, что изменение размеров обрабатываемых заготовок тоже происходит по закону прямой линии.
При изменении случайной величины X в интервале от a до b плотность f (x) постоянна и равна С; вне этого интервала она равна нулю. Так как площадь, ограниченная кривой распределения, равна единице
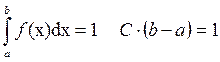 , отсюда
, отсюда 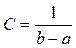 . (1.52)
. (1.52)
Плотность распределения f (x) имеет вид:
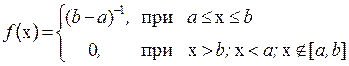 . (1.53)
. (1.53)
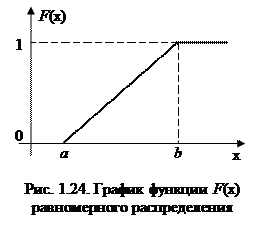
Функция распределения (рис. 1.24) и интенсивность отказов (рис. 1.23) имеют вид:
|
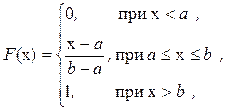 (1.54)
(1.54)
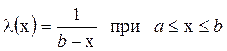 . (1.55)
. (1.55)
Вычислим математическое ожидание и дисперсию:
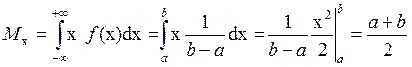 ,
,
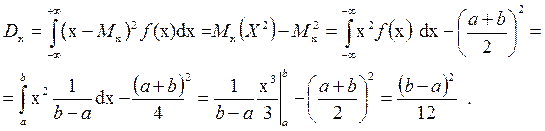
Определяем среднее квадратическое отклонение и поле рассеяния:
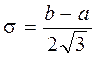 ;
; 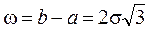 . (1.56)
. (1.56)
Коэффициент асимметрии Sk = 0 (распределение симметрично). Для определения коэффициента эксцесса найдем четвертый центральный момент
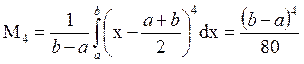 .
.
Отсюда 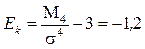 .
.
С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, погрешность дискретности в цифровых приборах и др. Равномерное распределение наиболее характерно для неисключенных систематических погрешностей. Если отсутствуют данные о виде распределения систематической погрешности, то они принимаются равномерными, так как оцениваются границами (пределами) допускаемых погрешностей.
 2015-05-20
2015-05-20 887
887








