Логарифмически нормальное распределение

Случайная величина Х имеет логарифмически нормальное распределение, если ее натуральный логарифм1n Х имеет нормальное распределение, параметры которого обозначим 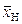и 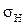. Основные характеристики этого распределения имеют вид:

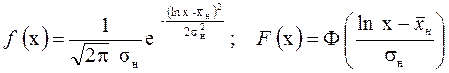. (1.48)

Среднее значение 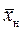и дисперсия 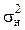выражаются с помощью параметров распределения по формулам:

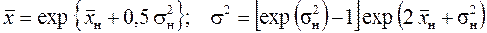. (1.49)

На рис. 1.21 изображены графики функций f (x) и l(х). Характерной особенностью логарифмически нормального распределения является то, что интенсивность отказов l (х) вначале увеличивается, а потом уменьшается (рис. 1.21,б).

Работать с логарифмически нормальным распределением удобнее, если свести его к хорошо известному нормальному распределению. Для этого следует рассматривать не случайную величину X, а ее логарифм1n X.