Это распределение при х > 0 задается следующими формулами:
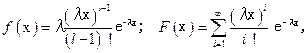 (1.44)
(1.44)
где l и l – параметры распределения, причем параметр l строго положителен, а l – целое положительное число.
Следует помнить, что частным случаем распределения Эрланга является экспоненциальное распределение (при l =1). Случайную величину X, имеющую распределение Эрланга с параметрами lи l, можно интерпретировать как сумму взаимно независимых случайных величин X 1, Х 2,.., Хl, имеющих экспоненциальное распределение с параметром l:
Х = Х 1 + Х 2 +... + Хl. (1.45)
Среднее значение 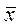 и среднеквадратическое отклонение s распределения Эрланга определяются по формулам:
и среднеквадратическое отклонение s распределения Эрланга определяются по формулам:
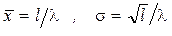 . (1.46)
. (1.46)
Графики плотности распределения f (х) при разныхзначениях l представлены на рис. 1.20. Интенсивность отказов l(х) в данном случае монотонно возрастает.
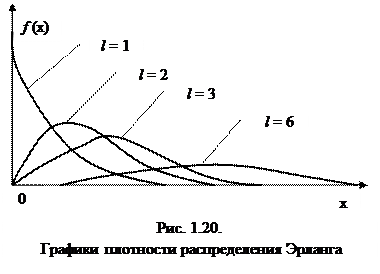 |
С ростом значения параметра l распределение Эрланга стремится к нормальному распределению. Это ясно из содержания центральной предельной теоремы теории вероятностей и представления по формуле (1.44). Поэтому при больших значениях l можно считать:
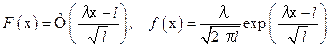 (1.47)
(1.47)
 2015-05-20
2015-05-20 1624
1624
