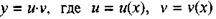2015-05-20
270
Пусть - дифференцируемые функции.
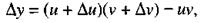Так как
 |
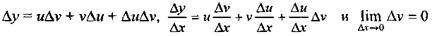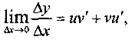на основании теоремы 2.1, то
откуда и следует формула (11)
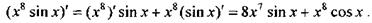Например,
Следствие 1. Постоянный множитель можно выносить за знак производной:
 |
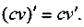(12)
Например,
 |
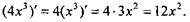Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные. Например,
 |
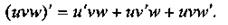Производная частного двух функций.
Теорема 4. 3
Производная частного двух дифференцируемых функций определяется формулой
 |
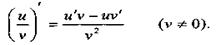(13)
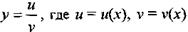Доказательство.
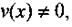Если - дифференцируемые функции, причем
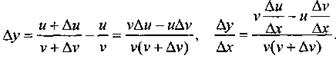то
 |
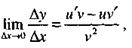Следовательно,
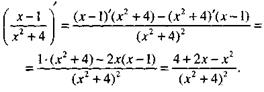так как 
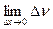на основании теоремы 2.1. Например,
