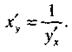Производная обратной функции

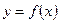Если и 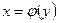- взаимно-обратные дифференцируе­мые функции и 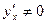, то

(14)

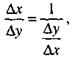Действительно, так как

то

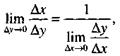откуда и следует равенство (14).

Производная сложной функции

Рассмотрим сложную функцию 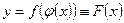, где 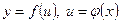; в этом случае и называют промежуточным аргументом, х - независимой переменной.

Теорема 4. 4

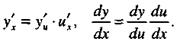Если 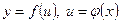— дифференцируемые функции своих аргументов, то производная сложной функции 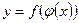существу­ет и равна произведению производной этой функции по промежуточ­ному аргументу на производную промежуточного аргумента по неза­висимой переменной, т.е.

(15)

Доказательство.

В соответствии с условием и по определению производной

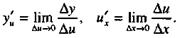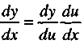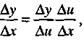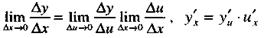Так как то или