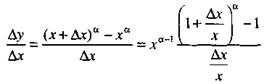Пример 3. Найти производную функции;; y = х 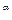, где - действительное число

Найти производную функции;; y = х , где 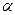- действительное число. Область определения степенной функции y = х 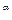зависит от 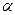. Составим отношение приращения функции к приращению аргумента:

и перейдем к пределу при 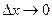, воспользовавшись формулой (10.50):

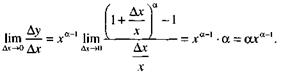
Следовательно,

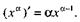
Отметим частные случаи этой формулы:

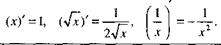
Основные правила дифференцирования.

Производная алгебраической суммы функций.

Теорема 4.1

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций.