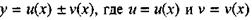Доказательство. Пусть - дифференцируемые функции

Пусть - дифференцируемые функции. Поскольку

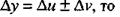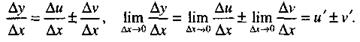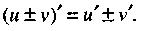Следовательно,

(10)

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

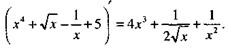Производная произведения функций.

Теорема 4.2

Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс про­изведение второй функции на производную первой, т.е.

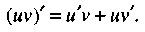(11)