Лемма о существовании вершины степени 5

Пусть – простой (т.е. без кратных ребер и петель), планарный граф, тогда в нем существует вершина, степень которой не превосходит 5.

Доказательство. Пусть 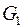– связная компонента планарного графа, 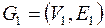, пусть 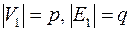. . 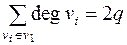Пусть 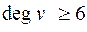для любой вершины 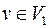, тогда 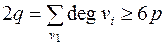. С другой стороны, в планарном графе без кратных ребер и петель 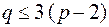, мы пришли к противоречию

,

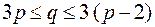что и доказывает лемму.