Пусть 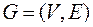 – двудольный граф,
– двудольный граф, 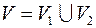 , где
, где 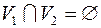 .
.
Определение. Паросочетанием называется произвольное подмножество попарно несмежных ребер двудольного графа.
Для графа, изображенного на рис. 34, паросочетанием будет,
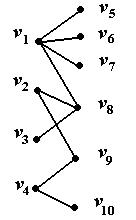 Рис. 34 Рис. 34 | например, множество 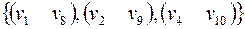 Пусть Пусть 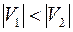 , тогда введем понятие совершенного паросочетания. Паросочетание будет совершенным, если в подмножество попарно несмежных ребер вошли все вершины множества , тогда введем понятие совершенного паросочетания. Паросочетание будет совершенным, если в подмножество попарно несмежных ребер вошли все вершины множества 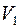 . Для графа, приведенного на рис. 34, совершенным паросочетанием будет, например, множество . Для графа, приведенного на рис. 34, совершенным паросочетанием будет, например, множество 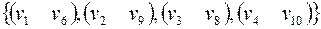 . . |
С совершенными паросочетаниями связано много прикладных задач, например, задача о составлении расписаний, задача о назначении на должность. Пусть 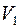 – множество должностей,
– множество должностей, 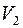 – множество претендентов, ребро
– множество претендентов, ребро 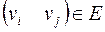 , если
, если 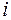 -тую должность может занимать
-тую должность может занимать 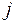 -й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания. Построить совершенное паросочетание удается не всегда (рис. 35).
-й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания. Построить совершенное паросочетание удается не всегда (рис. 35).
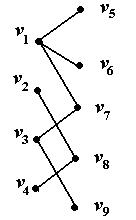 Рис. 35 Рис. 35 | Критерий существования совершенного паросочетания сформулировал и доказал Холл в 1935 г., он известен как теорема Холла о свадьбах. Пусть есть 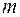 юношей и юношей и 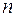 девушек, девушек, 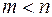 . Каждый из юношей знаком с какими-то девушками. Спрашивается, всегда ли можно женить этих юношей на знакомых им девушках. . Каждый из юношей знаком с какими-то девушками. Спрашивается, всегда ли можно женить этих юношей на знакомых им девушках. |
На языке теории графов задачу можно сформулировать так: 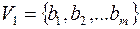 – множество юношей,
– множество юношей, 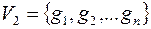 – множество девушек, если
– множество девушек, если 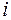 -тый юноша знаком с
-тый юноша знаком с 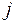 -той девушкой, то существует ребро
-той девушкой, то существует ребро 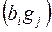 . Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
. Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
 2015-05-20
2015-05-20 1859
1859








