2015-05-20
582
Если в графе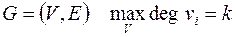 
, то граф 
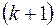– раскрашиваем.
Доказательство по индукции по числу вершин.
Если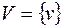 
, то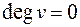 
и ее можно выкрасить одним цветом.
Пусть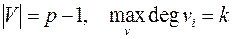 
и граф 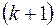– раскрашиваем.
Рассмотрим граф с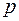 
вершинами, 
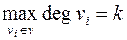. Удалим одну вершину со всеми инцидентными ребрами. Получим граф 
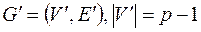и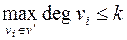 
. Тогда по индуктивному предположению граф 
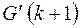– раскрашиваем. Добавим удаленную вершину со всеми инцидентными ребрами. Она будет иметь максимум 
смежных вершин, выкрасим ее в 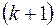– цвет, получим правильную раскраску графа 
.
Для раскраски планарного графа достаточно 5 цветов, правда, более 100 лет существует гипотеза «четырех красок», до сих пор не опровергнутая и не доказанная. Компьютерное моделирование планарных графов с числом вершин меньше 52 показало справедливость этой гипотезы для графов с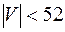 
.
Мы докажем теорему о достаточности 5 цветов для планарных графов, но прежде докажем лемму.
