Любой планарный граф без петель 5 - раскрашиваем.
Доказательство. При наличии петель граф не может быть правильно раскрашенным, так как концы любого ребра должны быть выкрашены в разные цвета.
При доказательстве теоремы мы воспользуемся леммой, в которой существенным требованием было отсутствие кратных ребер. Для правильной раскраски графа кратные ребра не играют никакой роли. На рис. 31 показано, что кратные ребра мы можем воспринимать как одно ребро.
Если граф несвязный, то задача сводится к правильной раскраске каждой связной компоненты.
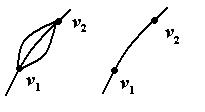 Рис. 31
Рис. 31
|
Пусть 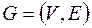 – простой планарный связный граф. Теорему будем доказывать по индукции, по числу вершин.
– простой планарный связный граф. Теорему будем доказывать по индукции, по числу вершин.
Пусть 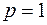 , тогда раскрасим эту вершину одним цветом.
, тогда раскрасим эту вершину одним цветом.
Пусть для графов с 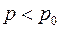 утверждение верно.
утверждение верно.
Пусть 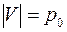 , рассмотрим геометрическую реализацию графа на плоскости. По лемме у графа существует вершина
, рассмотрим геометрическую реализацию графа на плоскости. По лемме у графа существует вершина  , такая, что
, такая, что 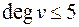 . Удалим эту вершину вместе с инцидентными ребрами, получим граф
. Удалим эту вершину вместе с инцидентными ребрами, получим граф 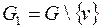 , он планарен, число вершин у него
, он планарен, число вершин у него 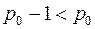 , по индуктивному предположению он 5-раскрашиваем.
, по индуктивному предположению он 5-раскрашиваем.
Вернем вершину  со всеми инцидентными ребрами. Пусть вершина
со всеми инцидентными ребрами. Пусть вершина  смежна с вершинами
смежна с вершинами 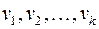 , где
, где 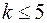 .
.
Возможны три варианта.
1. 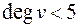 , т.е. она смежна с четырьмя или менее вершинами. Если даже все эти вершины выкрашены в разные цвета, то есть пятый цвет, в который можно выкрасить эту вершину.
, т.е. она смежна с четырьмя или менее вершинами. Если даже все эти вершины выкрашены в разные цвета, то есть пятый цвет, в который можно выкрасить эту вершину.
2. 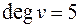 , но среди цветов вершин, с которыми смежна вершина
, но среди цветов вершин, с которыми смежна вершина  , есть повторяющиеся цвета, тогда вновь остается запасной цвет для вершины
, есть повторяющиеся цвета, тогда вновь остается запасной цвет для вершины 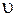 .
.
3. 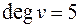 и все вершины, смежные с ней, выкрашены в разные цвета.
и все вершины, смежные с ней, выкрашены в разные цвета.
Занумеруем вершины, смежные с  и обозначим цвет вершины
и обозначим цвет вершины 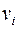 через
через 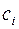 , как показано на рис. 32. Пусть
, как показано на рис. 32. Пусть 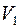 – связное множество вершин, до которых можно дойти из вершины
– связное множество вершин, до которых можно дойти из вершины 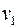 , идя по вершинам цветов
, идя по вершинам цветов 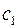 и
и 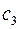 .
.
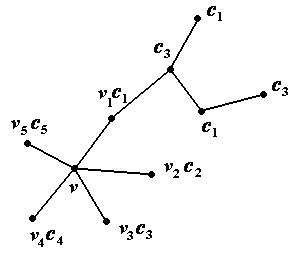 Рис. 32
Рис. 32
|
Вершина 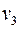 либо войдет в
либо войдет в 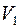 , либо нет. Рис. 32 иллюстрирует именно этот случай. Тогда в множестве
, либо нет. Рис. 32 иллюстрирует именно этот случай. Тогда в множестве 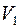 поменяем цвета
поменяем цвета 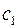 на
на 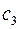 и
и 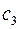 на
на 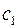 . При этом раскраска графа останется правильной, так как в
. При этом раскраска графа останется правильной, так как в 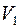 вошли все смежные вершины цветов
вошли все смежные вершины цветов 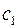 и
и 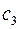 , но вершина
, но вершина 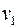 будет выкрашена в цвет
будет выкрашена в цвет 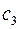 , тогда вершину
, тогда вершину  выкрасим в цвет
выкрасим в цвет 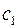 .
.
Если вершина 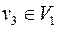 , как показано на рис. 33, то перекрашивать вершины в множестве
, как показано на рис. 33, то перекрашивать вершины в множестве 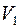 в этом случае бесполезно.
в этом случае бесполезно.
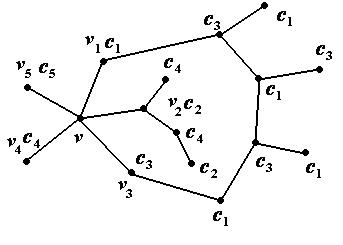 Рис. 33
Рис. 33
|
Тогда рассмотрим множество 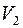 – связное множество вершин, до которых можно дойти из вершины
– связное множество вершин, до которых можно дойти из вершины 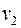 , идя по вершинам цветов
, идя по вершинам цветов 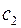 и
и 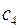 . Вершина
. Вершина 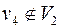 (рис. 33), так как она отделена от вершины
(рис. 33), так как она отделена от вершины 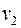 циклом. Путь из
циклом. Путь из 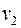 в
в 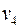 не может пересечь ребро – мы рассмотрели геометрическую реализацию графа на плоскости. Этот путь не может пройти и через вершину цикла, поскольку все вершины цикла окрашены в цвета
не может пересечь ребро – мы рассмотрели геометрическую реализацию графа на плоскости. Этот путь не может пройти и через вершину цикла, поскольку все вершины цикла окрашены в цвета 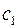 и
и 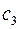 .
.
Поменяем в множестве 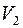 цвета
цвета 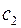 на
на 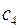 ,
, 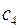 на
на 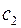 и выкрасим вершину
и выкрасим вершину  в цвет
в цвет 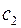 .
.
С задачей о раскраске графа связана, например, задача о раскраске географической карты, где соседние страны должны быть выкрашены в разные цвета. Странам сопоставим вершины графа, соседним странам соответствуют смежные вершины, которые должны быть выкрашены в разные цвета. Полученный граф будет плоским, следовательно, для его правильной раскраски достаточно пяти цветов.
 2015-05-20
2015-05-20 560
560








