Доказательство проводим по индукции по числу юношей.
1. 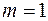 , так как по условию каждый юноша знаком по крайней мере с одной девушкой, женим его на ней.
, так как по условию каждый юноша знаком по крайней мере с одной девушкой, женим его на ней.
2. Пусть теорема верна для любого числа юношей меньше 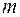 , при условии, что любые
, при условии, что любые  юношей знакомы не менее чем с
юношей знакомы не менее чем с  девушками.
девушками.
3. Докажем, что она верна для 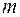 юношей.
юношей.
Рассмотрим 2 случая:
а) Пусть любые  юношей знакомы в совокупности не менее чем с
юношей знакомы в совокупности не менее чем с 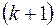 девушкой (т.е. условие теоремы выполняется с запасом). Тогда берем
девушкой (т.е. условие теоремы выполняется с запасом). Тогда берем 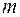 – того юношу и женим его на любой знакомой девушке. Остались
– того юношу и женим его на любой знакомой девушке. Остались 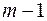 юноша, причем любые
юноша, причем любые  из них знакомы не менее, чем с
из них знакомы не менее, чем с  девушками. По индуктивному предположению, их можно женить.
девушками. По индуктивному предположению, их можно женить.
б) Существует группа из 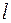 юношей, знакомых ровно с
юношей, знакомых ровно с 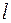 девушками
девушками 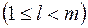 . Причем по условию теоремы, любые
. Причем по условию теоремы, любые  из этих
из этих 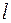 юношей знакомы не менее, чем с
юношей знакомы не менее, чем с  девушками,
девушками, 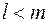 , по индуктивному предположению этих юношей можно женить на знакомых девушках.
, по индуктивному предположению этих юношей можно женить на знакомых девушках.
Осталось 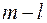 юношей, это меньше, чем
юношей, это меньше, чем 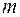 , но надо проверить, что любые
, но надо проверить, что любые  из этих
из этих 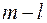 юношей знакомы не менее, чем с
юношей знакомы не менее, чем с  девушками из числа оставшихся (мы ведь часть девушек забрали, это могли быть знакомые оставшихся юношей). Только в этом случае мы сможем воспользоваться индуктивным предположением.
девушками из числа оставшихся (мы ведь часть девушек забрали, это могли быть знакомые оставшихся юношей). Только в этом случае мы сможем воспользоваться индуктивным предположением.
Пусть существуют 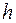 юношей из числа оставшихся, которые знакомы менее, чем с
юношей из числа оставшихся, которые знакомы менее, чем с 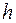 девушками из числа оставшихся. Тогда рассмотрим группу из этих
девушками из числа оставшихся. Тогда рассмотрим группу из этих 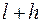 юношей и получим, что эта группа изначально была знакома менее, чем с
юношей и получим, что эта группа изначально была знакома менее, чем с 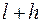 девушками, что противоречит условию теоремы.
девушками, что противоречит условию теоремы.
Следовательно, по индуктивному предположению, оставшихся 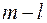 юношей можно женить на знакомых им девушках из числа оставшихся.
юношей можно женить на знакомых им девушках из числа оставшихся.
Замечание. Если 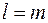 , это означает, что любая группа
, это означает, что любая группа  юношей числом меньше
юношей числом меньше 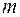 знакома не менее, чем с
знакома не менее, чем с 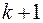 девушкой и только ровно
девушкой и только ровно 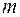 юношей знакомы с
юношей знакомы с 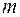 девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается
девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается 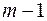 юноша, из которых любые
юноша, из которых любые  знакомы не менее, чем с
знакомы не менее, чем с  девушками, т.е. приходим в ситуацию а).
девушками, т.е. приходим в ситуацию а).
Для графов теорему Холла можно сформулировать так: построить совершенное паросочетание в графе можно тогда и только тогда, когда любые  вершин множества
вершин множества 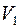 смежны в совокупности не менее, чем с
смежны в совокупности не менее, чем с  вершинами множества
вершинами множества 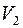 .
.
Для графа на рис. 35 условие теоремы Холла не выполняется: вершины 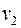 и
и 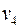 смежны только с одной вершиной.
смежны только с одной вершиной.
 2015-05-20
2015-05-20 493
493








