В ориентированном графе 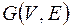 множество
множество 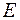 состоит из упорядоченных пар
состоит из упорядоченных пар 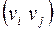 , которые называются дугами или ориентированными ребрами, вершина
, которые называются дугами или ориентированными ребрами, вершина 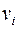 – начало дуги,
– начало дуги, 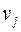 – ее конец (рис. 36).
– ее конец (рис. 36).
 Рис. 36
Рис. 36
| Полустепенью исхода вершины  называется число дуг, исходящих из называется число дуг, исходящих из  , она обозначается , она обозначается 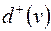 . Полустепенью захода вершины . Полустепенью захода вершины  , , 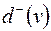 , называется число дуг, входящих в , называется число дуг, входящих в  . .
|
Если каждую упорядоченную пару 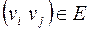 заменить неупорядоченной парой, мы получим неориентированный граф
заменить неупорядоченной парой, мы получим неориентированный граф 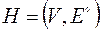 , ассоциированный с ориентированным графом
, ассоциированный с ориентированным графом  .
.
Говорят, что вершина  ориентированного графа (или орграфа) достижима из вершины
ориентированного графа (или орграфа) достижима из вершины 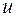 , если существует ориентированный путь из вершины
, если существует ориентированный путь из вершины 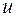 в вершину
в вершину  .
.
Орграф называют сильно связным, если любая вершина в нем достижима из любой другой вершины. Орграф называют односторонне связным, если для любых двух вершин 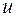 и
и  по крайней мере одна достижима из другой. Наконец, орграф называют слабо связным, если ассоциированный с ним граф является связным, в противном случае ориентированный граф называют несвязным.
по крайней мере одна достижима из другой. Наконец, орграф называют слабо связным, если ассоциированный с ним граф является связным, в противном случае ориентированный граф называют несвязным.
Если 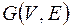 – орграф, то обратным к нему ориентированным графом будет граф
– орграф, то обратным к нему ориентированным графом будет граф 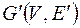 , где дуга
, где дуга 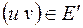 тогда и только тогда, когда дуга
тогда и только тогда, когда дуга 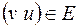 .
.
Вершина  ориентированного графа
ориентированного графа  называется источником, если из нее достижима любая другая вершина графа. Стоком в ориентированном графе
называется источником, если из нее достижима любая другая вершина графа. Стоком в ориентированном графе  называется любая вершина
называется любая вершина  , являющаяся источником в обратном к графу
, являющаяся источником в обратном к графу  графе
графе 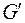 .
.
Направленным графом называется такой орграф, который не имеет ориентированных циклов длины 2, т.е. направленный граф не может содержать одновременно дуги  и
и 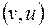 . Орграф называется полным, если любые 2 вершины связаны хотя бы одной дугой. Полный направленный граф называется турниром.
. Орграф называется полным, если любые 2 вершины связаны хотя бы одной дугой. Полный направленный граф называется турниром.
 2015-05-20
2015-05-20 1010
1010








